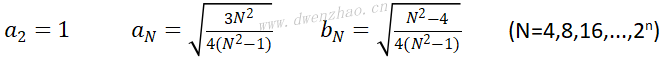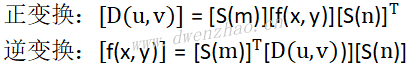图像处理与人工智能
图像变换域处理是将空间域图像信号转换到另外一种特征空间进行处理的方式,一般使用正交函数或正交矩阵对原图像作二维线性可逆变换,比如使用傅里叶变换转化为振幅、频率和相位函数的线性叠加,把图像从空间域变换到频率域,然后在频率域进行处理。频率域处理主要用于图像恢复、图像重建、辐射变换、边缘增强、图像锐化、图像平滑、噪声抑制、频谱分析、纹理分析等。
变换后的图像往往更有利于特征抽取、增强、压缩和图像编码。常用的图像变换方式有傅里叶变换、离散余弦变换、沃尔什变换、Gabor变换和小波变换等。
1. 傅里叶变换:
傅里叶变换是一种单一分辨率的信号分析方法,使用一固定短时窗函数。
1)连续傅里叶变换:
傅里叶变换是常用的正交变换,可以把信号从时域变换到频域。一维傅里叶变换公式为:
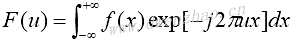
傅里叶变换结果是一个复数表达式。傅里叶逆变换为:
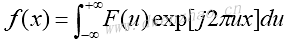
把傅里叶变换推广到二维,二维的傅里叶变换及逆变换公式为:
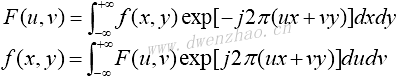
2)离散傅里叶变换:
为了让傅里叶变换用于计算机处理,需要将连续变换转变成离散变换。离散傅里叶变换公式:
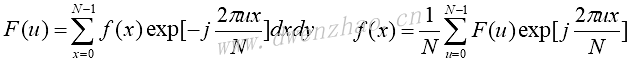
可以写成矩阵形式:
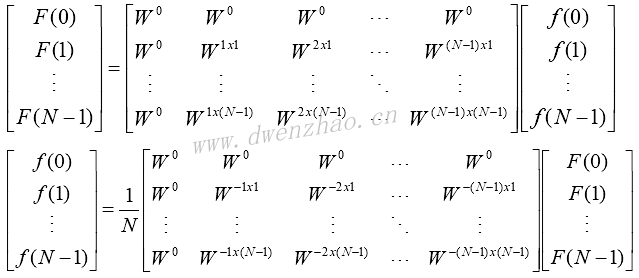
其中,W=exp[2π/N]
3)二维离散傅里叶变换:
二维离散函数f(x,y)的傅里叶变换为:
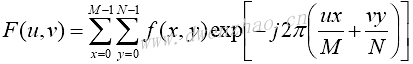
傅里叶逆变换为:
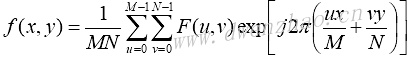
其中,x=0,1,2,...,M-1,y=0,1,2,...,N-1。
4)快速傅里叶变换:
傅里叶变换的计算量很大,运算次数正比于N2。Cooley和Tukey在1965年提出了一种逐次加倍的快速傅里叶变换算法FFT,使用该算法可以将运算次数降到正比于N。
设N=2L,L为正整数。按n为奇数和偶数将序列{f(n)}进行划分,记:
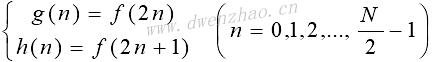
则离散傅里叶变换可以改写为:
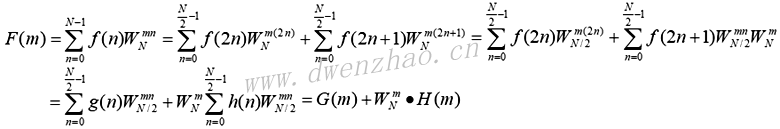
其中,G(m)和H(m)分别是g(n)和h(n)的离散傅里叶变换DFT。上式表明,一个长度为N的DFT可以转化为两个长度N/2的DFT。二维FFT可由两次一维FFT得到。
5)傅里叶变换的特性:
对图像的二维离散傅里叶变换,变换结果的左上、右上、左下、右下4个角的部分对应图像的低频成分,而中央部分对应高频成分。若想使低频成分出现在中央位置,可以使用傅里叶变换的平移特性。
①可分离性:
一个二维离散傅里叶变换,可以通过先后两次运用一维傅里叶变换来实现。
②平移性:
将f(x,y)乘以一个指数项相当于将二维傅里叶变换F(u,v)的频域中心移动到新的位置;而将F(u,v)乘以一个指数项相当于将f(x,y)的空域中心移动到新的位置。

也就是,空域中f(x,y)产生移动在频域只发生相移,而傅里叶变换的幅值不变;反之,当频域F(u,v)产生移动时,相应的f(x,y)在空域也只发生相移,而幅值不变。
在数字图像处理中,常常需要将F(u,v)的原点移到N×N方阵的中心,以便能清楚分析傅里叶变换频谱的情况,这时可以令u0=v0=N/2,而:
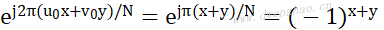
也即:
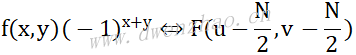
如果需要将图像频谱的原点从起始点(0,0)移到图像的中心点(N/2,N/2),只要将f(x,y)乘上(-1)x+y因子进行傅里叶变换即可实现。
③周期性:
傅里叶变换和反变换均以N为周期,也就是只须一个周期内的变换就可以将F(u,v)完全确定。
④共轭对称性:
如果f(x,y)是实函数,其傅里叶变换具有共轭对称性:
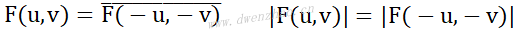
⑤旋转不变性:
如果f(x,y)在空域旋转θ角度,相应的傅里叶变换F(u,v)在频域也旋转同一角度θ。
⑥分配性:
傅里叶变换对于加法可以分配,而对乘法则不行。即:
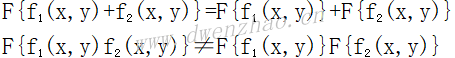
⑦比例性:
对于两个标量a和b,有:
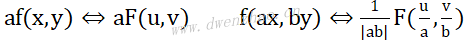
说明,在空间比例尺度的展宽对应于频域比例尺度的压缩,其幅值也减小为原来的1/|ab|。
6)傅里叶变换在图像处理中的应用:
频域上的高频信息对应着空域上变化比较剧烈的信号,而低频信号对应着空域上变化比较缓慢的信号,也即低频部分反应图像概貌,高频部分反应图像细节。一幅图像的傅里叶变换的幅频特性在其幅频图的四个角对应着空域的低频信息,而中心区域则对应着高频信息,一般来说,图像的大部分信息为低频信息,因此四角上比较亮而中心比较暗。为了方便观察,通常将幅频图进行四个对角置换,使低频部分集中在中心部分。
对图像进行频域处理,可以将信号的信息强度重新分配,比如可以通过高通滤波器将图像中的景物细节提取出来,通过低通滤波器可以将图像的概貌信息提取出来。利用图像的低频信息可以大幅压缩图像数据,而且能保存原图像的轮廓。
经过傅里叶变换后,频域和空域成为一对对偶关系,空域上的卷积对应着其在频域上的点乘,即:
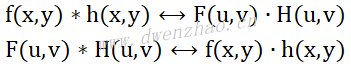
根据以上原理。当需要对图像进行滤波处理时,可以先将原图像和滤波器分别进行傅里叶变换,然后在频域进行点对点的乘积运算,最后将运算结果进行傅里叶反变换。
2. 离散余弦变换:
傅里叶变换需要计算复数,比实数运算费时,数据量也是实数的两倍。离散余弦变换DCT是从一种特殊形式的傅里叶变换转化而来,当原始信号满足一定条件时,可以将傅里叶变换转化成余弦变换。
1)一维离散余弦变换:
一维离散余弦变换定义为:
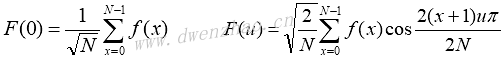
式中,F(u)是第u个余弦变换系数,u是广义频率变量,u=0,1,2,...,N-1。
一维离散余弦逆变换为:
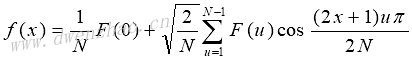
计算时先计算离散点数,对时域空间进行延拓,将时域点写入已开辟存储空间,调用快速傅里叶变换,调整系数,转换变换结果,将变换结果转存回时域存储区。利用FFT快速计算DCT时要对函数f(x)进行延拓:
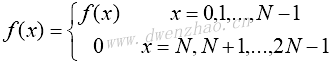
记
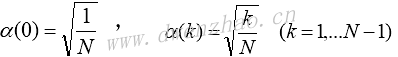
根据一维DCT定义,并利用Euler公式,得:
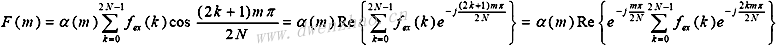
其中,Re{}表示取花括号内部复数的实部。上式将计算DCT转化为FFT的计算。
2)二维离散余弦变换:
二维离散余弦变换的定义为:
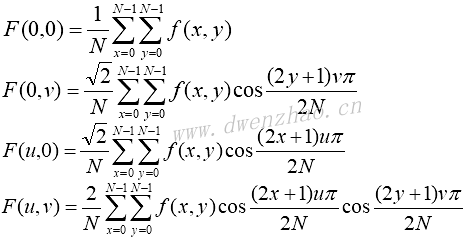
其中,f(x,y)为空间域二维向量,F(u,v)为变换系数矩阵。可见,二维离散余弦变换是可分离的,可通过两次一维变换实现,传统的行列方法是先沿行进行一维离散余弦变换,再沿列计算一维离散余弦变换。
二维离散余弦逆变换为:
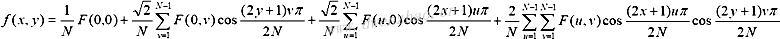
3)离散余弦变换的矩阵表示:
对一维离散余弦变换:

二维离散余弦变换:
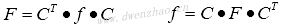
式中:
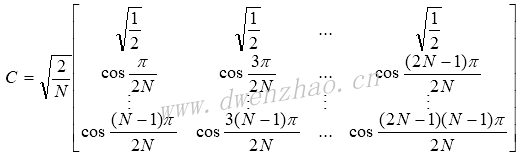
C是一个正交矩阵,C·CT=E,E为单位矩阵。
3. 离散沃尔什-哈达玛变换:
离散沃尔什变换是由两个值+1和-1为基本函数的级数展开而形成,满足完备的正交性。由于沃尔什函数是二值正交函数,适用于计算机处理。
1)沃尔什函数系:
沃尔什函数系函数值是仅取+1和-1两值的非正弦型标准正交完备函数系,其中的前10个函数见下图:
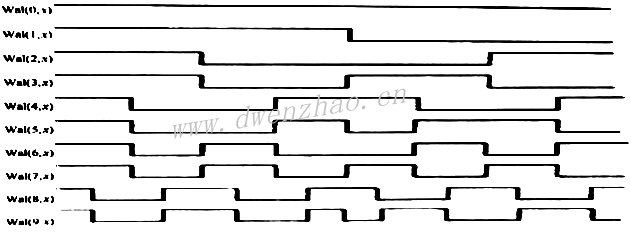
沃尔什函数是美国科学家沃尔什在1923年提出的理论,安照排列顺序,可以分为3种,按列率排序的沃尔什排列、按自然排序的佩利排列、哈达玛排列,即列率、佩利Paley和哈达玛Hadamard三种排列或编号方式。哈达玛排序的沃尔什函数是由2n阶哈达玛矩阵得到的,高阶矩阵可用两个低阶矩阵的克罗内克积求得,也称离散沃尔什-哈达玛变换。
p=3的哈达玛序的离散沃尔什函数的矩阵形式为8x8矩阵:

设最低阶(X=2)的哈达玛序的离散沃尔什函数矩阵为:
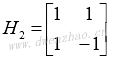
递推关系式为:
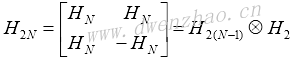
由此可以产生任意的2n阶哈达玛矩阵。
离散哈达玛变换是将离散序列的各项值的符号按一定规律改变后,进行加减运算,比复数运算的DFT要简单很多。
沃尔什变换的排列方式为列率排列,与正弦波频率相对应,列率表示某种函数在单位区间上函数值为0的个数之半。
2)沃尔什变换:
①一维离散沃尔什变换:
设f(x)表示N点的一维离散序列,则一维沃尔什变换定义为:
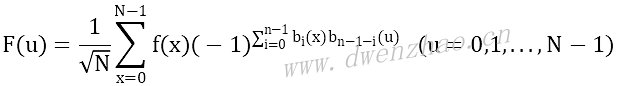
式中,N为沃尔什变换的阶数,N=2n;bi(z)为z的二进制数的第i位数值,取0或1。比如,i=6,二进制数为110,因此b0(z)=0,b1(z)=1,b2(z)=1。
一维沃尔什变换的正反变换核相同,因此计算沃尔什变换的算法可直接用来计算其逆变换。
一维沃尔什变换有快速算法,简称FWT。当N=8时,其变换核矩阵为:

②二维离散沃尔什变换:
设f(x,y)表示M×N的二维离散序列,则二维沃尔什变换定义为:
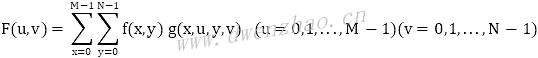
式中,二维离散沃尔什变换核为:
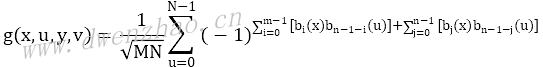
式中,M=2m,N=2n。
二维离散沃尔什变换的变换核是可分离的:
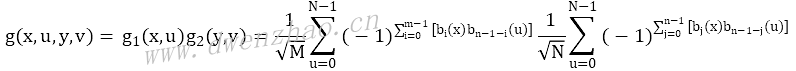
也就是二维沃尔什变换可以通过两次一维沃尔什变换来实现。
3)离散哈达玛变换:
哈达玛变换定义简单,存在从低阶到高阶的递推关系,高阶矩阵可以由两个低阶矩阵之积求得,便于快速运算,实用性更好。采用哈达玛排列的沃尔什函数进行的变换称为沃尔什-哈达玛变换WHT,或哈达玛变换。
哈达玛变换矩阵是仅由+1和-1两个元素组成的正交方阵,其任意两行或两列彼此正交,即它们的对应元素之和为0。哈达玛变换核矩阵与沃尔什变换的差异仅仅是行的次序不同。
一维哈达玛正变换:
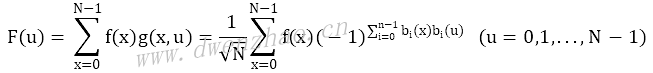
式中,g(x,u)为一维哈达玛变换的核,定义为:
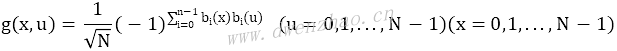
式中,N为哈达玛变换的阶数,N=2n,bi(z)为z的二进制数的第i位数值,取值0或1。
一维哈达玛逆变换的核与正变换相等。
哈达玛变换的阶数具有规律性,即按照N=2n规律递升,高阶哈达玛矩阵可以通过低阶哈达玛矩阵的克罗尼积运算求得:
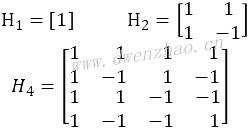
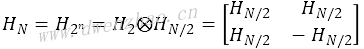
采用上述规律求哈达玛变换矩阵要比直接使用哈达玛变换核求矩阵快很多,这提供了一种快速哈达玛变换,可称为FHT。这样可以得出8阶哈达玛矩阵:

①一维定序哈达玛变换:
在哈达玛变换矩阵中,通常将某一列元素符号改变的总次数称为这个列的列率,上面给出的变换矩阵H8的8个列的列率分别为0、7、3、4、1、6、2、5。而定序哈达玛变换的变换矩阵的列率是随u的增加而递增的。如N=8时,定序哈达玛变换矩阵的列率从第1列到第8列分别为0、1、2、3、4、5、6、7。
当N=2n,定序哈达玛变换核与逆变换核相同,为:
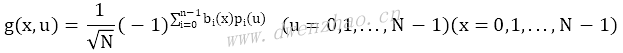
pi(u)按下列递推关系求得:
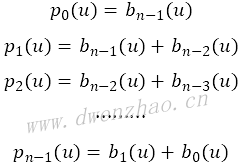
②二维定序哈达玛变换:
一维哈达玛变换可推广到二维,二维哈达玛变换的核与逆变换的核相等。二维哈达玛变换是可分离核对称的,因此一次二维哈达玛变换也可以分为两次一维哈达玛变换计算。二维哈达玛变换也有相应的定序哈达玛变换。
4)图像的离散沃尔什-哈达玛变换:
设M=2m,N=2n,对于图像MxN图像f(n,m),二维离散沃尔什-哈达玛变换W(u,v)定义为:
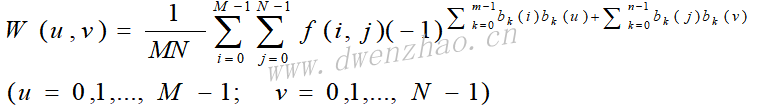
二维离散沃尔什-哈达玛逆变换定义为:
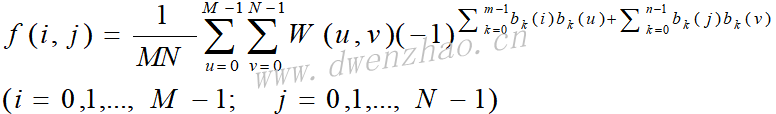
4. Gabor变换:
对Fourier变换预先加窗,时频谱反映时间局部特性,这就是短时Fourier变换,又称Gabor变换。Gabor变换是短时Fourier变换中当窗函数取为高斯函数时的一种特殊情况,可以在频域不同尺度和不同方向上提取相关特征。Gabor变换本质上还是对二维图像求卷积,对图像进行二维卷积等价于对图像的二维傅里叶变换及核函数的二维傅里叶变换在频域求乘法,通过二维傅里叶变换可以提高卷积的运算效率。
Gabor变换是图像表示中一种较好的模式,能达到交叉熵的最低边缘,能最好兼顾信号在时域和频域的分辨率,而且人的视觉对这种函数有很好匹配性,所以适用于图像滤波、纹理识别、边缘检测与提取、图像分割与识别。要实现Gabor变换,主要解决如何选择Gabor基函数和计算展开系数问题。
很多有用的窗函数都可以用来作为Gabor基函数,可以是时域表示,也可以是频域表示。最常用的窗函数是矩形函数和高斯函数。
矩形函数:
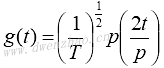
其中,
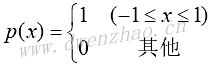
高斯函数:
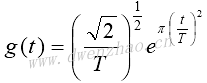
5. K-L变换:
当变量之间存在一定相关关系时,可以通过原始变量的线性组合,构成较少的不相关的新变量代替原始变量,而每一个新变量都包含尽量多的原始变量的信息,这种处理方法称主成分分析PCA,新变量称原始变量的主成分。主成分分析是寻找任意统计分布的数据集合主要分量的子集,使数据样本的互相关性降低到最低点。
离散卡胡南-洛夫(Karhunen-Loeve)变换简称K-L变换,基于主成分分析理论,以图像的统计特征为基础的最优正交线性变换,其变换矩阵由图像阵列的协方差矩阵的特征值和特征向量决定,也称特征向量变换。
6. SVD变换:
SVD是奇异值分解变换,是一种对非对称矩阵的正交变换,变换的结果矩阵是有一子块为对角矩阵,而其余阵元均为零。
从矩阵论角度,奇异值分解定义为:
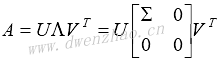
图像的奇异值变换在图像特征提取、压缩、检索、匹配、数字水印等领域应用广泛。
7. 斜变换:
斜变换是图像处理中另一种正交变换,非常适合于表示灰度逐渐改变的图像信号,已经用于图像编码。
1)斜矩阵:
斜向量是在一个在其范围内呈均匀阶梯下降的离散锯齿波形,可用S(n)表示为NxN斜矩阵:
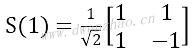
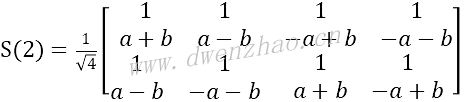
因为斜矩阵是由列向量构成的,所以根据高度均匀的条件,有:
(a+b)-(a-b)=(a-b)-(-a+b)=(-a+b)-(-a-b)
即a=2b
再根据矩阵为正交的条件,有:
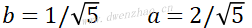
代入上式得到:
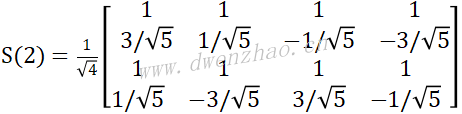
改写为另一种形式:
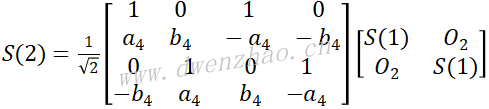
其中:
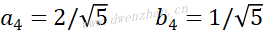
继而推导出:

因此得到一般式:

其中,I2为2x2的单位矩阵:
2)斜变换:
采用斜矩阵作为变换矩阵进行的正交变换称为斜变换。
设原图像为f(x,y),是一个MxN(M=2m,N=2n)的矩阵,D(u,v)为变换系数矩阵,斜变换可以表示为:
7. 小波变换简介:
小波变换是一种时间-尺度分析方法,而且具有多分辨率的特点,在处理时所进行的是空域和频域的局部变换,在时频两域都具有表征信号局部特征的能力,在低频段具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,适合探测正常信号中夹带的瞬态反常现象。
小波分析的多尺度分析特性提供了更灵活的处理办法,可以选择任意的分解层数,用尽可能少的计算量得到满意的结果。因此,小波变换能更有效地从图像中提取出信息,并且可通过缩放、平移等对图像进行多尺度细化分析,实现自适应分析,甚至可以根据需要而聚焦到图像的任意细节。
小波系数与原始图像存在着空间上的对应关系,这对于滤波处理很有利,通过了解小波系数的分布情况,利用不同的滤波器处理小波系数,经过逆变换后可以得到理想的处理结果。比如,经过两次小波分解后,图像轮廓主要体现在左上角的低频部分,细节部分体现在高频部分。对于一幅图像,表现一个图像最主要的部分是低频部分,一个最简单的压缩方法是利用小波分解,去掉图像的高频部分而只保留低频部分,也可以通过对低频分解系数进行增强处理而对高频分解系数进行衰减处理而达到增强的效果。
一幅图像做小波变换分解后,不同分辨率的子图像对应的频率是不同的。小波一次变换实际就是图像既进行行行变换又进行行列变换,结果是最上角显示缩小为原来四分之一的图像,右上角是图像行变换结果,左下角是图像列变换的结果,而右下角则是图像进行45°边缘检测的处理结果。小波二次变换实际上就是在小波一次变换的基础上,对处理好的低频带图像再进行一次小波一次变换,结果是图像缩小为十六分之一。一般所说的小波变换仅对低通滤波器的输出递归进行。如果不仅对低通滤波器的输出进行递归分解,而且也对高通滤波器的输出进行递归分解,称为小波包变换。
小波变换不仅保持原图像的空间特性,而且提取了图像的高频信息;小波分量有方向选择性,分为水平、垂直和斜向,与人的视觉特征吻合;能量主要集中于低频子带图像;水平子带在水平方向相关系数大,而垂直方向小;垂直子带在垂直方向相关系数大,而水平方向小;斜子带在垂直方向和水平方向相关系数都小。 小波变换有连续小波变换、小波级数展开和离散小波变换。
1)一维连续小波变换:
对于任意函数f(x),其连续小波变换的数学定义为:
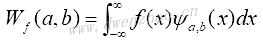
对于任意实数对(a,b),小波母函数能够通过平移和伸缩基本小波ψ(x)来生成:
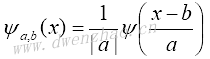
其中,a为尺度因子,b为平移因子。通常情况下,基本小波ψ(x)以原点为中心,因此平移后就以x=b为中心。
连续小波逆变换为:
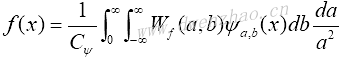
2)二维连续小波变换CWT:
若f(x,y)是一个二维函数,则它的连续小波变换为:
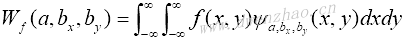
其中,bx、by表示在两个维度上的平移。二维连续小波逆变换为:
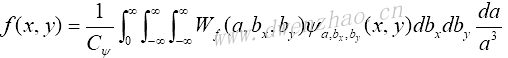
其中:
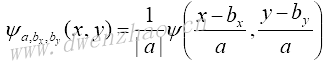
而ψ(x)是一个二维基本小波。
3)一维离散小波变换:
计算机上实现时,连续的小波必须进行离散化处理。离散化是针对尺度参数a和连续平移参数b而言,离散化取样后:
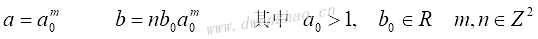
连续小波的离散化形式为:
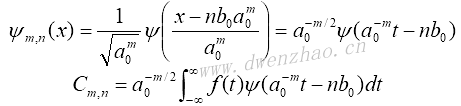
离散小波变换式是一种时频分析,它从集中在某个区间上的基本函数开始,以规定步长向左或向右移动基本波形,并用尺度因子a0来扩张或压缩以构造其函数系,一系列小波由此而生。这里m和n分别成为频率范围指数和时间步长指数。
如果尺度以二进方式离散化,可得到相应的二进小波变换:
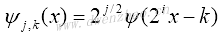
整数j决定伸缩,而k决定平移幅度。其中变换系数再次由内积给出:
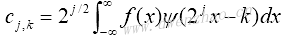
4)二维离散小波变换:
要在图像处理中使用小波变换,就必须将小波从一维推广到二维。二维基本小波为:
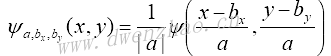
假定存在可分离的二维尺度函数Φ(x,y)=Φ(x)ψ(y),其中Φ(x)为一维尺度函数,ψ(y)为相应的小波函数,则可以得到三个二维基本小波变换函数:
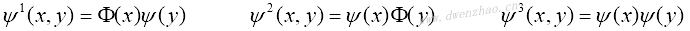
由此建立小波变换的基础。其中的上标只是索引。
一幅NxN的图像fj(x,y),下标j指示尺度,为2的幂。对于j=1,原图像的尺度为2的0次幂为1。j值的每一次增大都使尺度加倍,分辨率减半。每一次通过隔行隔列采样,图像被分解为4个大小为原来尺寸四分之一的子频带区域,这4个子频带区域的每一个都由原图与一个小波基内积后,再经过x和y方向都进行2倍的间隔抽样而产生的。每一个层次都分解而构成4个在尺度2的j+1次幂上的更小图像。内积可以写成卷积形式。
因为尺度函数和小波函数都是可分离的,所以每个卷积都可以分解成行列上的一维卷积。DWT图像分解步骤为:
在第一层,首先用h0(-x)和h1(-x)分别与图像fj(x,y)的每行做积分并丢弃奇数列;接着,这个NxN/2阵列的每一列再和h0(-x)和h1(-x)相卷积,丢弃奇数行,其结果就是该层变换所要求的4个(N/2)x(N/2)的数组。
5)小波变换分解算法:
小波变换分解算法为:
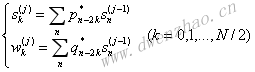
重构算法通过下式实现:

其中,pk和qk分别为低通滤波器和高通滤波器的系数。
实际编程中,用f(k)作为![]() ,可进行逐级小波分解,Db8的8个低通滤波器系数为:
,可进行逐级小波分解,Db8的8个低通滤波器系数为:
h[0]=0.230377813309, h[1]=0.714846570553, h[2]=0.630880767930,
h[3]=-0.027983769417, h[4]=-0.187034811719, h[5]=0.030841381836,
h[6]=0.032883011667, h[7]=-0.010597401785
8个高通滤波器系数为:
g[7]=0.230377813309, g[6]=-0.714846570553, g[5]=0.630880767930,
g[4]=0.027983769417, g[3]=-0.187034811719, g[2]=-0.030841381836,
g[1]=0.032883011667, g[0]=0.010597401785
⑴小波行变换:
小波行变换的方法是先将图像的偶数列存入图像缓存左半部分,将图像奇数列存入图像缓存右半部分,然后用一阶或二阶微分算子进行垂直方向的边缘检测,比如用奇数列依次减去它前面的偶数列,再将差分结果进行调整,存入图像缓存右半部分。
⑵小波列变换:
小波列变换的方法是先将图像的偶数行存入图像缓存上半部分,将图像奇数行存入图像缓存下半部分,然后用一阶或二阶微分算子进行水平方向的边缘检测,比如用奇数行依次减去它前面的偶数行,再将差分结果进行调整,存入图像缓存下半部分。
⑶小波变换:
小波一次变换就是对图像既进行行变换又进行列变换,其结果是最上角显示缩小为原来四分之一的图像,右上角是图像的行变换结果左下角是图像的列变换结果,而右下角则是图像进行45°边缘检测的处理结果。小波二次变换就是在小波一次变换的基础上,对处理好的低频带再进行一次小波变换,其结果是图像缩小为十六分之一。一般所说的小波变换,仅对低通滤波器的输出递归进行,如果不仅对低通滤波器的输出进行递归分解,而且也对高通滤波器的输出进行递归分解,则称为小波包变换。
操作步骤为:开辟两个图像缓冲区tmp1和tmp2,tmp1的左半部分存储图像偶数列数据,tmp2右边部分存储图像奇数列数据;将tmp1奇数列的数据分别依次减去其前面的偶数列,并将结果存入tmp右半部分;tmp2的上半部分存储tmp1的偶数行数据,tmp2的下半部分存储tmp1的奇数行数据;将tmp2奇数行的数据分别依次减去其前面的偶数行,并将结果存入tmp2的下半部分;将tmp2的数据保存到源数据区。
6)小波基:
小波基是由尺度滤波函数和小波函数组成,定义数据结构时需要定义逆变换滤波器。离散小波变换利用两个滤波器h(n)和g(n),编程实现中又可以分为整型变换和浮点型变换,定义数据结构时要分别定义正变换滤波器和逆变换滤波器的整型数据和浮点型数据,还需要定义正逆变换的偏移量。C代码示例:
typedef struct{
double *cH;
int nH;
double *cHtildel
int nHtilde;
int offH,offG,offHtilde,offGtilde;
}waveletfilter;
有了上面的小波数据结构后,就可以利用来定义多种小波基。
①Battle-Lemarie小波基:
该小波基有两种形式,一种不保证变换的可逆性和正交性,另一种则是可逆的且保证小波基的正交性。编程实现中一般考虑后一种小波基。
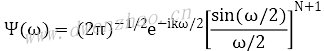
式中,当N为奇数时,k=0;当N为偶数时,k=1。小波函数为尺度函数的对称转置。
其中高通滤波器定义:
static double cHBattleLemarie[]={
M_SQRT2*-0.002,
M_SQRT2*-0.003,
M_SQRT2*0.006,
M_SQRT2*0.006,
M_SQRT2*-0.013,
M_SQRT2*-0.012,
M_SQRT2*0.030,
M_SQRT2*0.023,
M_SQRT2*-0.078,
M_SQRT2*-0.035,
M_SQRT2*0.307,
M_SQRT2*0.542,
M_SQRT2*0.307,
M_SQRT2*-0.035,
M_SQRT2*-0.078,
M_SQRT2*0.023,
M_SQRT2*0.030,
M_SQRT2*-0.012,
M_SQRT2*-0.013,
M_SQRT2*0.006,
M_SQRT2*0.006,
M_SQRT2*-0.003,
M_SQRT2*-0.002,
0.0
};
滤波器定义中,M_SQRT2是一个双精度浮点型常量:
#define M_SQRT2 1.41421356237309504880168872420969808
完整小波基定义:
waveletfilter wfltrBattleLemarie={
cHBattleLemarie,
N_ELEM(cHBattleLemarie),
cHBattleLemarie,
N_ELEM(cHBattleLemarie),
/*下面4个数据分别定义了滤波器H和G,以及逆变换系数H'和G'的偏移量*/
11,11,11,11
};
其中,N_ELEM是定义的一个宏函数,其实现为:
#define N_ELEM(st)(sizeof(st)/sizeof((st)[0]))
②Haar小波基:
Haar小波基是最常用的小波基,其尺度函数与小波函数定义分别为:
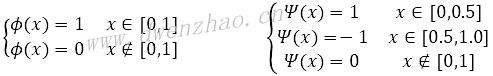
Haar小波基的定义:
//高通滤波器定义,即尺度函数
static double cHHaar[]={
M_SQRT2*1.0/2.0,
M_SQRT2*1.0/2.0
};
//完整小波基定义
waveletfilter wfltrHaar={
cHHaar,
N_ELEM(cHHaar),
cHHaar,
N_ELEM(cHHaar),
/*下面4个数据分别定义了滤波器H和G,以及逆变换系数H'和G'的偏移量*/
0,0,0,0
};
③Daubechies小波基系列:
Haar小波基是Daubechies小波基系列中的特例。其定义为:
假设存在有:
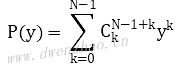
其中C是二项式系数。则有:
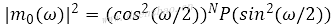
同时满足:
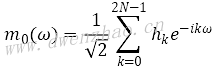
那么Daubechies小波基系列是由系数CμN来确定尺度函数和小波函数的,它们都必须满足上面的公式。Daubechies4是常量N=4时小波基的定义:
//定义宏常量
#ifndef SQRT3
#define SQRT3 1.73205080756887729352745
#endif
//高通滤波器定义,即尺度函数
static double cHDaubechies_4[]={
M_SQRT2*(1+SQRT3)/8.0,
M_SQRT2*(3+SQRT3)/8.0,
M_SQRT2*(3-SQRT3)/8.0,
M_SQRT2*(1-SQRT3)/8.0
};
//完整小波基定义
waveletfilter wfltrDaubechies_4={
cHDaubechies_4,
N_ELEM(cHDaubechies_4),
cHDaubechies_4,
N_ELEM(cHDaubechies_4),
/*下面4个数据分别定义了滤波器H和G,以及逆变换系数H'和G'的偏移量*/
1,1,1,1
};
④Coiflet小波基:
Coiflet小波基是在Daubechies小波基基础上发展起来的,其尺度函数和小波函数具有很好的对称性。Coiflet2型小波基的定义:
//定义宏常量
#ifndef SQRT15
#define SQRT15 3.87298334620741688517927
#endif
//高通滤波器定义,即尺度函数
static double cHCoiflet_2[]={
M_SQRT2*(SQRT15-3)/32.0,
M_SQRT2*(1-SQRT15)/32.0,
M_SQRT2*(6-2*SQRT15)/32.0,
M_SQRT2*(2*SQRT15+6)/32.0,
M_SQRT2*(SQRT15+13)/32.0,
M_SQRT2*(9-SQRT15)/32.0
};
//完整小波基定义
waveletfilter wfltrCoiflet_2={
cHCoiflet_2,
N_ELEM(cHCoiflet_2),
cHCoiflet_2,
N_ELEM(cHCoiflet_2),
/*下面4个数据分别定义了滤波器H和G,以及逆变换系数H'和G'的偏移量*/
3,1,3,1
};
上述是最常用的小波基,此外还有包括样条函数为基础的小波基,以及双正交小波基等。
7)小波基的基本操作:
①小波基翻转和转换:
函数将小波基滤波器函数的正变换与逆变换的参数进行转换,处理对象基于双正交小波基的转换,对正交小波基不做处理。
//输入 waveletfilter *wfltrNorm,原小波滤波器
//输出 waveletfilter *wfltrRev,转换函数输出
//若wfltrNorm=wfltrRev则满足转换条件,即双正交小波基
void wfltr_exchange(wfltrNorm,wfltrRev){
int iSwap;
double *pDSwap;
iSwap=wfltrNorm->offH;
wfltrRev->offH=wfltrNorm->0ffHtilde;
wfltrRev->0ffHtilde=iSwap;
//高通滤波器转换
iSwap=wfltrNorm->nH;
wfltrRev->nH=wfltrNorm->nHtilde;
wfltrRev->nHtilde=iSwap;
//低通滤波器转换
iSwap=wfltrNorm->offG;
wfltrRev->offG=wfltrNorm->offGtilde;
wfltrRev->offGtilde=iSwap;
pDSwap=wfltrNorm->cH;
wfltrRev->cH=wfltrNorm->cHtilde;
wfltrRev->cHtilde=pDSwap;
return;
}
②小波的细化:
小波的细化等同于小波变换的逆变换,它利用指定的小波基滤波器通过滤波操作来完成。细化的步骤实际上是将小波基进行一次重建。
⑴细化迭代:
/*函数输入:
waveletfilter *wfltr: 小波函数滤波器
TYPE_ARRAY *a: 细化小波基的存储空间
int n: 小波基大小,必须是2的指数值*/
static void wrefine_step(wfltr,a,n)
waveletfilter *wfltr;
TYPE_ARRAY *a;
int n;
{
int nDiv2=n/2;
int i,iHtilde,j,iA;
TYPE_ARRAY *aNew;
(void)MALLOC_LINTOK(aNew,n,TYPE_ARRAY);
for (i=0;i<n;i++)
aNew[i]=0.0;
for(j=0;j<nDiv2;j++){
for (iHtilde=0;iHtilde<wfltr->nHtilde;iHtilde++){
iA=MOD(2*j+iHtilde-wfltr->offHtilde,n);
aNew[iA]+=wfltr->cHtilde[iHtilde]*a[j];
}
}
for(i=0;i<n;i++)
a[i]=aNew[i];
FREE_LINTOK(aNew);
return;
}
⑵一维小波细化:
/*函数输入:
TYPE_ARRAY *a: 输入原始数据,用于细化的小波基数据
int nA: 数据A的大小,必须是2的指数值
int nNew: 细化后小波基大小,必须是2的指数值
waveletfilter *wfltr: 需要细化的小波滤波器
TYPE_ARRAY *aRefined: 函数输出,细化后数据*/
void FUNC_1D(a,nA,nNew,wfltr,aRefined)
TYPE_ARRAY *a;
int nA;
int nNew;
waveletfilter *wfltr;
TYPE_ARRAY *aRefined;
{
int iA;
double scale;
assert(nA<=nNew);
for (iA=0;iA<nA;iA++)
aRefined[iA]=a[iA];
for (iA=2*nA;iA<=nNew;iA*=2)
wrefine_step[wfltr,aRefined,iA];
scale=sqrt(RATIO(nNew,nA));
for (iA=0;iA<nNew;iA++)
aRefined[iA]*=scale;
return;
}
⑶多维小波细化:
/*函数输入:
TYPE_ARRAY *aO: 输入原始数据,用于细化的小波基数据
int nAO: 每一维上数据aO的大小,必须是2的指数值
int nDim: 小波基的维数以及数组nAO[]的大小
bool isFwd: 小波基是否完整正交
waveletfilter *wfltr: 需要细化的小波滤波器
int nAR[]: 细化后小波基每一维的大小,必须是2的指数值
TYPE_ARRAY *aR: 函数输出,细化后数据*/
void FUNC_ND(aO,nAO,nDim,isFwd,wfltr,nAR,aR)
TYPE_ARRAY *aO;
int nAO;
int nDim;
bool isFwd;
waveletfilter *wfltr;
int nAR[];
TYPE_ARRAY *aR;
{
int k;
int iDim,nAOTotal,nAOMax,nARMax;
int iO1,iO2,iO3,nO,nONext;
int nOPrev=1;
int nRPrev=1;
int nR,nRNext;
TYPE_ARRAY *aOTmp,*aRTmp;
nAOMax=1;
nARMax=1;
nAOTotal=1;
for(iDim=0;iDim<nDim;iDim++){
if (nAO[iDim]>nAOMax)
nAOMax=nAO[iDim];
if (nAR[iDim]>nARMax)
nARMax=nAR[iDim];
nAOTotal*=nAO[iDim];
}
//临时数据空间要足够大,保证最大维数小波基细化
(void)MALLOC_LINTOK(aOTmp,nAOMax,TYPE_ARRAY);
(void)MALLOC_LINTOK(aRTmp,nARMax,TYPE_ARRAY);
for(iDim=0;iDim<nDim;iDim++){
nO=nAO[nDim-1-iDim];
nR=nAR[nDim-1-iDim];
nONext=nO*nOPrev;
nRNext=nR*nRPrev;
if (nO>=MIN_ORDER){
for (iO2=0;iO2<nAOTotal;iO2+=nONext){
for (iO1=0;iO1<nAOPrev;iO1++){
//将相关的行列及小波基其他信息复制
iO3=iO1+iO2;
for (k=0;k<nO;k++){
aOTmp[k]=aO[iO3];
iO3+=nOPrev;
}
//调用一维小波基细化函数
FUNC_1D(aOTmp,nO,nR,wfltr,aRTmp);
//将细化结果从数据空间中粘贴至输出小波基
i3=i1+i2;
for (k=0;k<nR;k++){
aR[i3]=aRTmp[k];
i3+=nRPrev;
}
}
}
}
nOPrev=nONext;
nRPrev=nRNext;
}
FREE_LINTOK(aRTmp);
FREE_LINTOK(aOTmp);
return;
}
③小波变换的实现:
⑴一维离散小波变换函数:
/*函数输入
TYPE_ARRAY *a: 原始的输入数组,即存放信号信息数组
int nA: 小波基大小,必须为2的指数倍
bool isFwd: 判定是否为正变换
waveletfilter *wfltr:用于小波变换的滤波器
TYPE_ARRAY *aXf: 小波变换后的系数存放空间*/
void FUNC_1D(a,nA,isFwd,wfltr,aXf)
TYPE_ARRAY *a;
int nA;
bool isFwd;
waveletfilter *wfltr;
TYPE_ARRAY *aXf;
{
assert(aTmp1D==NULL);
//分配数据空间
(void)MALLOC_LINTOK(aTmp1D,nA,TYPE_ARRAY);
//完成整个小波变换的函数实体
wxfrm_1d_varstep(a,1,nA,isFwd,wfltr,aXf);
//释放临时数据空间
FREE_LINTOK(aTmp1D);
aTmp1D=NULL;
return;
}
⑵小波变换的实现:
/*函数输入
TYPE_ARRAY *aIn: 输入的原始数据
int incA: 数组aIn[]和aXf[]元素之间的间隔大小
int nA: 小波基大小,必须为2的指数倍
bool isFwd: 判定是否为正变换
waveletfilter *wfltr:用于小波变换的滤波器
TYPE_ARRAY *aXf: 小波变换后的系数存放空间*/
void wxfrm_1d_varstep(aIn,incA,nA,isFwd,wfltr,aXf)
TYPE_ARRAY *aIn;
int incA;
int nA;
bool isFwd;
waveletfilter *wfltr;
TYPE_ARRAY *aXf;
{
int iA;
if(nA<MIN_ORDER)
return
if(isFwd){
//变换由最高层开始,然后逐渐往最小层进行变换
wfltr_convolve(wfltr,isFwd,aIn,incA,nA,aXf);
for(iA=nA/2;iA>=MIN_ORDER;iA/=2)
wfltr_convolve(wfltr,isFwd,aXf,incA,iA,aXf);
}else{
//如果是逆变换从最小层开始,然后逐渐往最大层进行
if(aXf!=aIn){
for(iA=0;iA<=nA;iA++)
aXf[incA*iA]=aIn[incA*iA];
}
for(iA=MIN_ORDER;iA<=nA;iA*=2)
wfltr_convolve(wfltr,isFwd,aXf,incA,iA,aXf);
}
return;
}
⑶小波变换过程中的卷积计算:
离散小波变换实际上是通过卷积计算完成的。
/*函数输入
waveletfilter *wfltr:用于卷积计算的小波滤波器
bool isFwd: 判定是否为正变换
TYPE_ARRAY *aIn: 输入数据,正变换时为信号信息,逆变换时为小波系数
int incA: 数组aIn[]和aXf[]元素之间的间隔大小
int n: 数组aIn[]和aXf[]的大小
TYPE_ARRAY *aXf: 小波变换后的系数存放空间*/
static void wfltr_convolve(wfltr,isFwd,aIn,incA,n,aXf)
waveletfilter *wfltr;
bool isFwd;
TYPE_ARRAY *aIn;
int incA;
int n;
TYPE_ARRAY *aXf;
{
int nDiv2=n/2;
int iA,iHtilde,iGtilde,j,jH,jG,i;
double sum;
bool flip;
//H为小波变换的高通滤波器,G为用于信号的细化分析滤波器
//Htilde为用于逆变换的高通滤波器,Gtilde为用于逆变换的细化分析滤波器
//Gtilde是正变换滤波器H的镜像滤波器
int nGtilde=wfltr->nH;
//正变换滤波器G是Htilde的镜像滤波器
int nG=wfltr->nHtilde;
if(isFwd){
/*正变换算法:
aTmp1D[0..n/2-1]=H*a (低频成分)
aTmp1D[n/2..n-1]=G*a (高频细节成分)*/
for(i=0;i<nDiv2;i++)
//数组aTmp1D[0..nDiv2-1]包含的是信号的低频成分
sum=0.0;
for(jH=0;iH<wfltr->nH;iH++){
iA=MOD(2*i+jH-wfltr->offH,n);
sum+=wfltr->cH[jH]*aIn[incA*iA];
}
aTmp1D[i]=sum;
//数组aTmp1D[nDiv2..n-1]包含的是信号的细节成分
sum=0.0;
flip=TRUE;
for(jG=0;iG<wfltr->nH;iG++){
iA=MOD(2*i+jG-wfltr->offG,n);
if(flip)
sum-=wfltr->cHtilde[nG-1-jG]*aIn[incA*iA];
else
sum+=wfltr->cHtilde[nG-1-jG]*aIn[incA*iA];
flip=!flip;
}
aTmp1D[nDiv2+i]=sum;
}
}else{
/*逆变换算法:
aTmp1D=Htilde^t*aIn[0..n/2-1]
+Gtilde^t*aIn[n/2..n-1]*/
for(i=0;i<n;i++)
aTmp1D[i]=0.0;
for(j=0;j<nDiv2;j++)
for(iHtilde=0;iHtilde<wfltr->nHtilde;iHtilde++){
iA=MOD(2*j+iHtilde-wfltr->offHtilde,n);
aTmp1D[iA]+=wfltr->cHtilde[iHtilde]*aIn[incA*j];
}
flip=TRUE;
for(iGtilde=0;iGtilde<wfltr->nGtilde;iGtilde++){
//逆变换中,假设小波系数是周期性的
iA=MOD(2*j+iGtilde-wfltr->offGtilde,n);
if(flip)
aTmp1D[iA]-=wfltr->cH[nGtilde-1-iGtilde]*aIn[incA*(j+nDiv2)];
else
aTmp1D[iA]+=wfltr->cH[nGtilde-1-iGtilde]*aIn[incA*(j+nDiv2)];
flip=!flip;
}
}
}
for(i=0;i<n;i++)
aXf[incA*i]=aTmp1D[i];
return
}