赵工的个人空间

图像的变换、滤波、增强分割、边缘检测及图像复原、压缩等，是相对复杂的处理过程。

一、图像正交变换：

图像二维正交变换在数字图像处理中经常使用，比如傅里叶变换域中，高频分量往往对应图像的边缘，利用这一特性可以从图像中抽取特征。傅里叶变换后，能量往往集中在少数项上，或者说能量集中在低频分量上，所以通过对低频分量分配较多的比特数，对高频分量分配较少比特数，即可实现图像数据压缩。

1. 傅里叶变换：

傅里叶变换应用非常广泛，如图像特征提取、空间频率域滤波、图像恢复、纹理分析等。二维傅里叶变换有很多重要性质，线性、可分性、共轭对称性、旋转性、比例变换特性、能量守恒、相关定理、卷积定理、空域平移性、频域平移性等。

1）快速傅里叶变换FFT：
二维离散傅里叶变换可以由两步一维离散傅里叶变换来实现。FFT算法以N的组成情况可以分成N为2的整数幂的算法、N为高复合数的算法、N为素数的算法三种情况。
⑴ 一维快速傅里叶变换fft：
MATLAB中一维快速傅里叶变换函数fft调用格式为：
Y=fft(X) ---- 返回向量X的离散傅里叶变换。若X为矩阵，fft函数返回矩阵每列的傅里叶变换；若X为多维数组，fft函数计算第一个非单元素的维。
Y=fft(X, n) ---- 返回n点傅里叶变换。若lenght(X)小于n，X将被在末尾添加0到n长度；若lenght(X)大于n，X按顺序在顶端被截断。当X为矩阵，矩阵的每列都被调整成同形式。
Y=fft(X, [], dim) ---- 在维数dim上应用fft算法
Y=fft(X, n, dim)
⑵ 二维快速傅里叶变换fft2：
Y=fft2(X) ---- 返回二维离散傅里叶变换，结果Y和X大小相同，等价于fft(fft(X).').'
Y=fft2(X, m, n) ---- 变换前把X截断或者添加0成mxn的数组，返回结果大小为mxn
⑶ 对n维数组的快速傅里叶变换fftn：
Y=fftn(X) ---- 返回X的多维离散傅里叶变换，结果Y和X大小相同
Y=fftn(X, siz) ---- 通过把X用0补齐或者截断多余的办法创建一个大小为size的多维数组，然后计算其傅里叶变换，结果Y的大小为siz。
等价于：
Y=X;
for p=1:length(size(X))
Y=fft(Y, [], p);
end
⑷ 把傅里叶变换的零频率部分移到频谱的中间fftshift：
Y=fftshift(X) ----把fft函数、fft2函数和fftn函数输出的结果的零频率部分移到数组的中间
Y=fftshift(X, dim) ---- 把fftshift操作应用到dim维上
对于向量，fftshift把X左右部分交换一下；对于矩阵，fftshift把X的一、三象限和二、四象限交换；对于高维数组，fftshift在每维交换X的半空间。
⑸ 傅里叶逆变换：
上述傅里叶变换函数对应的逆变换函数分别为：ifft、ifft2、ifftn、fftshift，与傅里叶变换的格式类似。
使用傅里叶变换，把需要做的卷积运算转换到频域中做乘法运算，然后再逆变换。根据傅里叶变换的相关性，可以在图像中定位目标图，也即模式匹配。通常的做法是，将图像和旋转90°后的模式图像（定位目标图）做相关运算，然后对结果值取一定的阈值。

2. 离散余弦变换：

在傅里叶级数展开式中，如果函数对称于原点，则其级数中将只有余弦函数项。受这一现象启发，提出离散余弦变换discrete cosine transform，简写为DCT。余弦变换是实的正交变换，一个序列的余弦变换和经过对称扩展的DFT有关，因此DCT可直接由DFT算法求得；余弦变换对高度相关的数据具有良好的集中能量特性。
MATLAB提供了两种DCT变换的方法，一种是使用dct2函数，基于FFT算法可对输入大数组快速计算；第二种是使用DCT变换矩阵，变换矩阵由dctmtx函数获取，变换矩阵适合输入小型平分矩阵，如8x8矩阵、16x16矩阵等。
一个MxM的变换矩阵T，对于MxM矩阵A，T*A返回一个每列一维DCT变换的MxM矩阵。矩阵A的二维DCT变换可以写成B=T*A*T。T是一个标准正交实数矩阵，它的逆矩阵和转置矩阵相同，也就是B的二维DCT变换为T*B*T。
1）dct2函数：
B=dct2(A) ---- 返回矩阵A的二维离散余弦变换，矩阵B和A大小一致，变换系数B(k1,k2)
B=dct2(A, m, n) ---- 在变换前用0把A扩展到mxn的大小，若m或n比A对应维的小则截取
B=dct2(A, [m, n])
2）dctmtx函数：
D=dctmtx(n) ---- 返回nxn离散余弦变换矩阵
当A为nxn矩阵，D*A为矩阵A每列的DCT变换，D'*A为矩阵A每列的逆DCT变换

3. Walsh-Hadamard变换：

严格来说，Walsh和Hadamard是两种变换，但二者非常相似。Hadamard变换基向量的元素只取±1。Hadamard变换的基向量可以通过采样Walsh函数获取，Walsh函数是一组在[0 1]上定义的正交矩形函数。使用hadamard函数来实现变换。

4. Radon变换：

Radon函数是计算图像沿着指定方向上的投影，一个二元函数f(x, y)的投影为一个特定方向的线性积分。
1）Radon函数：
计算图像I在theta向量所指定方向上的Radon变换的函数为radon：
[R, xp]=radon(I, theta)
其中，I表示待处理的图像，theta表示Radon变换的方向角度，可以是一个标量或向量值。返回值R的每一列对应图像I在theta某个角度的Radon变换值，xp向量表示沿着x'轴对应的坐标值。图像I的中心在floor((size(I)+1)/2)，在x'轴上对应x'=0。
在计算很多角度的Radon变换时，通常把变换值显示为一个图像。
2）Radon变换检测直线：
可以利用radon函数来实现Hough变换，Hough变换常用于计算机视觉。实现步骤为：
·利用edge函数计算图像的二值边缘图像
·计算二值图像的Radon变换
·计算出Radon变换后的峰值，这些峰值就对应原始图像的直线
3）逆Radon变换：
iradon函数实现Radon逆变换，可以从投影数据中重构图像。调用格式：
IR=iradon(R, theta)
在求Radon逆变换时，是利用R各列中的投影值来构造图像I的近似值，使用的投影越多，所获取的图像越接近原始图像，失真越小。对于角度theta必须是固定增量的均匀向量，即每次角度增值为常数。若角度增值已知，可以作为参数取代theta值传入iradon函数。
投影含有噪声时，可以通过加窗消去高频噪声：
IR=iradon(R, theta, 'Ram-Lak') ---- 采用Ram-Lak滤波，缺省值
IR=iradon(R, theta, 'Shepp-Logan') ---- Shepp-Logan窗滤波，sinc函数生成Ram-Lak滤波器
IR=iradon(R, theta, 'Cosine') ---- 采用Cosine窗滤波，cosine函数生成Ram-Lak滤波器
IR=iradon(R, theta, 'Hamming') ---- 采用Hamming窗滤波，Hamming窗Ram-Lak滤波器
IR=iradon(R, theta, 'Hann') ---- 采用Hann窗滤波，Hann窗Ram-Lak滤波器
IR=iradon(R, theta, 0.90) ---- 允许指定归一化频率D，高于D的滤波器响应为0，整个滤波器压缩在[0 D]范围内。假如系统不含高频信息而存在高频噪声时可用来完全抑制噪声，又不影响图像重建。
MATLAB的Phantom函数可以产生Shepp-Logan的大脑图，可作为一个测试图。

5. Fan-Beam变换：

Fan-Beam投影也是指图像沿着指定方向上的投影，与Radon投影是平行光束不同，Fan-Beam投影是点光束，发散成一个扇形，称为扇形射线。
⑴ fanbeam函数：
fanbeam函数计算图像沿着指定方向上的投影，沿着光束发散路径扇形计算线性积分。调用格式：
F=fanbeam(I, D)
F=fanbeam(... , param1, val1, param2, val2, ...) ---- 表示输入的一些参数
[F, sensor_positions, fan_rotation_angles]=fanbeam(...) ---- 返回探测器和扇形旋转角度信息
其中，I表示需要Fan-Beam变换的图像，D表示光源到图像中心像素点的距离，
Fan-Beam函数的控制参数：

在使用fanbeam函数时需要指定一些参数，如图像、投影光束源点距离和旋转中心。射线数量由fanbeam函数根据图像大小和给定的一些参数来设定。缺省情况下，扇形束在离旋转中心距离D处，沿着探测器弧形1度的间隔分配发散光束。
⑵ ifanbeam函数：
从Fan-Beam变换数据重构图像，调用格式：
I=ifanbeam(F, D)
I=ifanbeam(... , param1, val1, param2, val2, ...) ---- 表示输入的一些参数
[I, H]=ifanbeam(...) ---- H为返回的频率响应滤波器
F表示二维Fan-Beam变换数据，每列数据对应一个旋转角度的Fan-Beam变换数据。ifanbeam假定的投影中心点是ceil(size(F, 1)/2)。
ifanbeam函数的控制参数：

若投影数据是由fanbeam函数计算得到的，那么重构图像可能和原始图像不一样大小。重构的效果与投影数相关，投影数越多投影重构的效果越好，为了重构出较高的图像效果，需要提高重构图像投影角度的数目。
⑶ Radon投影和Fan-Beam投影的转换：
MATLAB提供了两种投影之间转换的函数para2fan和fan2para，其调用方法与fanbeam /ifanbeam、radon/iradon函数调用方法类似。

二、图像滤波器：

滤波技术在图像复原和图像增强中有着广泛应用，可以通过滤波图像来增强图像的某个属性或去除一些属性。对图像处理，最常用的滤波器是FIR滤波器。

1. 线性滤波：

滤波器是指用来对输入信号进行滤波的硬件或软件。

1）卷积运算：
MATLAB提供了一些函数进行卷积或相关运算。
⑴ conv函数：
w=conv(u, v)
分别对矢量u和v求卷积，结果矢量的长度为LENGHT(A)+LENGTH(B)-1。如果u和v分别是多项式系数，卷积的结果等价于多项式的乘法。
⑵ conv2函数：二维卷积运算函数
C=conv2(A, B) ---- 计算数组A和B的二维卷积
C=conv2(hcol, hrow, A)
C=conv2(... , 'shape')
如果一个数组描述了一个二维FIR滤波器，则另一个数组被二维滤波。当A大小为[ma,na]、B大小为[mb,nb]，那么C的大小为[ma+mb-1,na+nb-1]。参数shape为：

⑶ convn函数：n维卷积函数
C=convn(A, B) ---- 计算数组A和B的n维卷积
C=convn(A, B, 'shape')
返回值C的大小为size(A)+size(B)-1。
⑷ corrcoef函数：互相关系数函数
R=corrcoef(X) ---- 返回互相关系数矩阵
R=corrcoef(x, y) ---- 如果x和y都是列向量，等价于R=corrcoef([x y])。
[R, P]=corrcoef(...)
[R, P, RLO, RUP]=corrcoef(...)
[...]=corrcoef(...) , 'param1', val1, 'param2', val2, ...)
矩阵X的每一行为一个样本，每列为一个向量。

2）imfilter滤波函数：
B=imfilter(A, H)
B=imfilter(A, H, option1, option2, ...)
其中，A为被滤波的图像数组或多维彩色图像数组，H为预定义的滤波算子。由于imfilter函数是基于邻域滑动设计而实现的，所以也会涉及边界填充问题。option参数可以有几种：
边界参数：

输出大小参数：

相关和卷积参数：

3）预定义滤波：
二维预定义的滤波器函数fspecial，调用格式：
h=fspecial(type)
h=fspecial(type, parameters)
函数的参数type有：

2. FIR滤波器设计：

二维FIR（Finite impulse response有限冲激响应）滤波器有很多优点：易于表征为系数矩阵，二维FIR滤波器是一维FIR滤波器的自然扩展，有多种成熟的滤波器设计方法，易于实现，能够设计成具有严格线性响应同时可以具有任意幅度特性，FIR滤波器的单位采样响应是有限长，具有稳定性。

1）计算二维频率响应fregz2函数：
[H, f1, f2]=freqz2(h, n1, n2) ---- 返回FIR滤波器h的n1xn2点频率响应矩阵H，默认值64。f1和f2为对应的频率轴矢量，取归一化频率[-1 1]，其中1对应采样频率的一半或π弧度。
[H, f1, f2]=freqz2(h, [n2 n1])
[H, f1, f2]=freqz2(h, f1, f2) ---- 返回指定频率坐标(f1, f2)处的频率响应H
[H, f1, f2]=freqz2(h) ---- 是[n2 n1]=[64 64]时的特殊情况
[...]=freqz2(h, ... , [dx dy]) ---- 用[dx dy]代替h中的采样点之间的间隔，dx确定x-维上的间隔，dy确定y-维上的间隔，默认间隔为0.5，对应2.0的采样频率
[...]=freqz2(h, ... , dx]) ---- 用dx确定两个坐标上的采样间隔
freqz2(...) ---- 无返回值，只生成二维幅频响应的网格图
输入矩阵数据可以是double类型或任何整型，其他输入的数据都要double类型，相应的输出都是double类型。

2）计算期望频率响应矩阵freqspace函数：
freqspace函数返回等间隔频率响应的隐含频率范围。因为滤波器设计函数fsample2、fwind1和fwind2都是基于期望频率响应矩阵来设计过滤器的，所以通常都要先调用freqspace函数。
[f1, f2]=freqspace(n) ---- 对应一个nxn矩阵，返回二维频率矢量f1和f2。当n为奇数时，f1和f2都是[-n+1:2:n-1]/n；当n为偶数时，f1和f2都是[-n:2:n-2]/n。
[f1, f2]=freqspace([m n]) ---- 从一个mxn的矩阵返回二维频率矢量f1和f2
[x1, y1]=freqspace(... , 'meshgrid') ---- 等价于[f1, f2]=freqspace(...); [x1, y1]=meshgrid(f1, f2)
f=freqspace(N) ---- 表示假设N个均匀分布在单位圆上的点，返回一维频率向量f，无论N是奇数或偶数，f都是(0:2/N:1)。当N是奇数时，返回(N+1)/2个点；当N为偶数时，返回(N+2)/2个点。
f=freqspace(N, 'whole') ---- 表示返回N个均匀分布在整个单位圆上的点，这种情况下，f是0:2/N:2x(N-1)/N

3）频率变换法：
频率变换法是通过频率变换将一个一维零相位FIR滤波器变换成二维滤波器，由于它保持了一维滤波器的大多数特性，因而如果一维滤波器是最优的，则变换得到的二维滤波器也容易保持最优性。通过频率变换得到的二维滤波器具有有效的实现结构，比直接用卷积法或者DFT实现的运算量要小。
函数ftrans2用于实现频率变换方法，此函数缺省的变换矩阵由近似圆对称的滤波产生，定义自己的变换矩阵可以获取不同对称性，频率变换方法通常会产生很好的响应结果。格式：
h=ftrans2(b, t) ---- 由相应一维FIR滤波器和变换矩阵t产生二维滤波器h
h=ftrans2(b) ---- 默认使用McClellan矩阵
b必须是一维、奇数长的FIR滤波器，变换矩阵t包含的系数详细说明了使用频率变换的情况。得到的滤波器h可以直接应用于函数fliter2。
McClellan矩阵为：

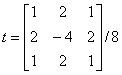
如果t矩阵大小为mxn，b的长度为Q，则h的大小为：

4）频率采样法：
频率采样法通过给出的定义频率响应形状的矩阵点来创建一个频率响应的滤波器。但这种方法没有约束给出定点间的频率响应的行为，通常在这些区域起波纹。MATLAB使用fsamp2实现频率采样设计二维FIR滤波器。格式为：
h=fsamp2(Hd) ---- 由频率响应Hd设计二维FIR滤波器，返回的滤波器系数保存在矩阵h中
h=fsamp2(f1, f2, Hd, [m n]) ---- 由匹配的向量点f1和f2滤波器响应产生一个mxn的FIR滤波器。频率向量f1和f2是归一化频率，其中1.0对应采样频率的一半或π弧度，结果滤波器尽可能逼近最少平方意义上的期望响应。为了得到最佳效果，至少需要mxn个期望频率点，如果少于mxn个点，函数即将报错。
矩阵Hd包含了在x和y频率轴的[-1.0 1.0]区间间隔点上的期望频率响应采样点，这里的1.0对应了采样频率的一半或π弧度，并且h和Hd的大小相同。函数返回的h可以直接应用于函数filter2。

5）窗函数法：
线性相位FIR滤波器通常采用窗函数法设计。窗函数法设计FIR滤波器基本思想是：根据给定的滤波器技术指标，选择滤波器长度N和窗函数ω(n)，使其具有最窄宽度的主瓣和最小的旁瓣。工程中常用的窗函数有6种，矩形窗、巴特利特窗Bartlett窗、汉宁Hanning窗、汉明Hamming窗、布莱克曼Blackman窗、凯塞Kaiser窗。
MATLAB提供两个窗函数设计滤波器的函数。
⑴ fwind1函数：
用指定的一个或两个一维窗函数构造成一个二维窗函数来设计二维滤波器。函数支持两种生成二维窗函数的方法：
·用单一的一维窗变换创建一个近似圆对称的二维窗函数（近似旋转的方法）
·计算两个一维窗外积生成一个矩形可分离的二维窗函数
h=fwind1(Hd, win) ---- 由频率响应Hd设计二维FIR滤波器
h=fwind1(Hd, win1, win2) ---- 用两个一维窗函数创建一个可分离的二维窗函数，若length (win1)=m，length(win2)=n，则返回值h大小为mxn。
h=fwind1(f1, f2, Hd, ...) ---- 指定沿着X和Y轴上任意频率的期望频率响应Hd，频率向量f1和f2元素值的范围是[-1.0 1.0]，其中1.0对应采样频率的一半或π弧度。
可以从MATLAB的信号处理工具箱的窗函数定义win，如boxcar、hamming、hanning、bartlett、blackman、kaiser、chebwin等。若length(win)=n，则h大小为nxn。矩阵Hd是在x和y频率轴范围[-1.0 1.0]上间隔点的期望频率响应采样得到的，为了得到精确的结果，Hd可以由freqspace函数返回的频率点获得。
⑵ fwind2函数：
直接由二维窗函数来设计二维滤波器。格式为：
h=fwind2(Hd, win) ---- 期望频率响应Hd的逆傅里叶变换与窗函数win的积生成二维FIR
h=fwind2(f1, f2, Hd, win) ---- 指定沿X和Y轴上任意频率的期望频率响应Hd，频率向量f1和f2元素值的范围[-1.0 1.0]，其中1.0对应采样频率的一半或π弧度。窗的长度控制了结果滤波器的大小，这里h和win的大小一致。
为了得到精确的结果，Hd可由freqspace函数返回的频率点得到。

三、图像增强：

图像增强是指按特定的需要突出一幅图像中的某些信息，同时消弱或去除某些不需要的信息的处理方法，主要目的是处理后的图像对某些特定的应用比用来的图像更加有效。图像增强技术主要包括直方图修改、图像平滑、图像尖锐化、彩色处理等。实际应用中，常常几种方法联合处理以达到预期的增强效果。
图像增强技术可分为频域处理和空域处理两类。频率处理的基础是卷积定理，它采用修改傅里叶变换的方法实现对图像的增强；空域处理是直接对图像中的像素进行处理，基本上以灰度映射变换为基础，比如增加图像的对比度、改善图像的灰度层次等。

1. 灰度变换增强函数：

MATLAB提供了一些返回图像数据值信息的统计特性的函数。

1）像素选择：
⑴ impixel函数：显示鼠标在图像选择像素点的颜色
P=impixel(I)
P=impixel(X, map)
P=impixel(RGB)

P=impixel(I, c, r)
P=impixel(X, map, c, r)
P=impixel(RGB, c, r)
[c, r, P]=impixel(...)

P=impixel(x, y, I, xi, yi)
P=impixel(x, y, X, map, xi, yi)
P=impixel(x, y, RGB, xi, yi)
[xi, yi, P]=impixel(...)
由c和r决定像素点对应的颜色值赋给返回值P；x与y均为二元素向量，指定图像的Xdata好Ydata；xi和yi为等长向量。缺省输入参数，则运算当前轴上的图像；没有输入参数可通过鼠标选择。可以显示两个像素点的欧几里得几何距离。
⑵ improfile函数：获取在图像上沿一条或多条路径所对应的像素点颜色值
c=improfile
c=improfile(n)
参数n为鼠标选择路径上指定的点数。返回值c为内插数据值，对灰度图像返回c为nx1元素向量，对于RGB图像返回的c为nx1x3数组。缺省c则绘出计算值图形。
根据选择路径情况，图形可能二维有可能三维。当不输入参数时，鼠标变成十字型，通过鼠标选择线段，输出所得线段灰度值或颜色值。
c=improfile(I, xi, yi)
c=improfile(I, xi, yi, n)
参数xi和yi为等长向量，指定线段末端的空间坐标。
[cx, cy, c]=improfile(...)
[cx, cy, c, xi, yi]=improfile(...)
参数cx和cy均为长度n的向量，其中包括要计算点的坐标。
[...]=improfile(x, y, I, xi, yi)
[...]=improfile(x, y, I, xi, yi, n)
参数x和y均为二元素向量，指定图像的XData和YData。
[...]=improfile(... , method)
指定插值方法。参数method为：
·nearest ：默认，最邻域插值
·bilinear ：双线性插值
·bicubic ：双立方插值
2）图像等值线imcontour函数：
绘制图像的等值线。调用格式：
imcontour(I, n) ---- 绘制灰度图像I等值线，n是图像灰度间隔等级的个数，即等值线个数
imcontour(I, v) ---- 绘图图像中由向量v指定的数据值等值线
imcontour(x, y, ...) ---- 参数x、y表示X轴和Y轴的范围
imcontour(... , LineSpec) ---- 参数LineSpec指定图形的点型、线性和颜色
[C, h]=imcontour(...)
3）图像直方图imhist函数：
绘制图像的直方图。调用格式：
imhist(I, n)
imhist(X, map) ---- map为色图
[counts, x]=imhist(...) ---- counts、x对应直方图数值与位置
其中，n为灰度图像灰度级，若I为灰度图像，缺省n=256；若I为二值图像，缺省n=2。
4）图像像素的统计特性：
图像像素统计特性函数有：
均值函数mean2：B=mean2(A) ---- 计算图像A的均值B
标准差函数std2：b=std2(A) ---- 计算图像A的标准差b
相关系数corr2：r=corr2(A, b) ---- 计算图像A和B的相关系数
5）imadjust函数：调整灰度值或色图
J=imadjust(I)
J=imadjust(I, [low_in;high_in], [low_out;high_out]) ---- 将灰度图像I转换成图像J
J=imadjust(I, [low_in;high_in], [low_out;high_out], gamma)
newmap=imadjust(map, [low_in;high_in], [low_out;high_out], gamma) ---- 索引图像色图变换
RGB2=imadjust(RGB1, ...) ---- 分别对每个图像板进行对应映射变换
值在[low_in;high_in]间的值对应于[low_out;high_out]，其他的值被剪切，并且把值分别置换成与low_out和high_out相对应，默认值为[0 1]。gamma用来描述变换函数曲线的形状，gamma<1增强亮度，gamma>1增强暗度，缺省gamma=1，表示线性变换。
对索引图像色图的变换中，如果low_in、high_in、low_out、high_out、gamma为标量，分别对红、绿、蓝三色进行变换；如果low_in、high_in、low_out、high_out为三元向量或gamma为三元向量，映射不同的颜色分别进行各自指定的变换。newmap与map大小一致。
6）brighten函数：把图像亮度增亮或变暗
brighten(beta)
brighten(h, beta)
newmap=brighten(beta)
newmap=brighten(cmap, beta)
若0<beta<1增亮图像，若-1<beta<0变暗图像。
7）histeq函数：直方图均衡增强亮度
J=histeq(I, hgram) ---- 转换灰度图像，是输出图像直方图具有length(hgram)个灰度级
J=histeq(I, n) ---- 将灰度图像转换成具有n个离散灰度级的灰度图像，n默认64
[J, T]=histeq(I, ...) ----返回I和J相对应的灰度变换函数
其中sum(hgram)=prod(size(I))
newmap=histeq(X, map, hgram) ---- 参数map对应操作的色图
newmap=histeq(X, map)
[newmap, T]=histeq(X, ...)
直方图均衡化后，灰度间隔被拉大，有利于图像的分析与识别。直方图均衡化处理方法采用的变换函数是累积分布函数，它产生一种近似均匀的直方图。理论上，直方图均衡化就是通过变换函数将原图的直方图调整为具有平坦倾向的直方图，然后用此均衡直方图校正图像。实际上，直方图均衡化后的图像直方图并不是十分均衡的，因为直方图上频数较小的某些灰度要加入一个或几个灰度级中。
8）直方图规定化：
有些情况下，并不总是需要图像有均匀直方图，而是需要有特定的直方图，以便对图像中的某些灰度级加以增强，这就是直方图规定化。直方图规定化的步骤为：
·用直方图均衡化方法将原图像进行均衡化处理
·规定希望的灰度概率密度函数，求出变换函数
·应用直方图均衡化方法进行逆变换

2. 空域滤波增强：

使用空域模板进行的图像处理称为空域滤波，模板称为空域滤波器。空域滤波从处理效果分类为平滑滤波器和锐化滤波器，平滑的目的在于消除混杂在图像中的干扰以改善图像质量，锐化的目的在于增强图像边缘以便图像识别和处理。
1）平滑滤波器：
可以使用filter2滤波函数，其中使用fspecial函数的average参数进行邻域平均平滑滤波。邻域平均法抑制了噪声，同时也由于平均而引起了模糊现象，模糊程度与邻域半径成正比。为了尽可能减少模糊失真，有人提出超限邻域平均法。
维纳滤波器是另一种线性平滑滤波器，这是一种自适应滤波器，能根据图像的区域方差来调整滤波器的输出。MATLAB使用wiener2实现维纳滤波器。格式为：
J=wiener2(I, [m n], noise) ---- 通过mxn模板计算图像的均值和标准方差，m和n缺省值3
[J, noise]=wiener2(I, [m n]) ---- 滤波前估算加性噪声
其中，noise为加性噪声。
高斯滤波器在空域内也有平滑功能，可以调用h=fspecial('gaussian')实现高斯滤波器。
2）中值滤波器：
中值滤波的原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代换。中值滤波器的窗口可以取方形、圆形、十字形等。数字图像中的值用邻域的最大值代换的滤波器，称为最大值滤波器；代换的值是最小值，称为最小值滤波器。
MATLAB中使用medfilt2函数实现中值滤波器。格式为：
B=medfilt2(A, [m n]) ---- 对图像A执行二维中值滤波，每个输出像素为mxn邻域的中值
B=medfilt2(A) ---- 为m和n缺省为3的情况
B=medfilt2(A, 'indexed', ...]) ---- 参数'indexed'表明操作对象为索引图像
在图像的边界用0填充图像，所以边缘的中值为[m n]/2区域的中值，可能失真。
medfilt2函数其实是调用ordfilt2函数来实现中值滤波的。调用格式：
B=ordfilt2(A, order, domain) ---- 通过邻域domain中非零元素形状的第order元素来置换A中的每个元素
B=ordfilt2(A, order, domain, S) ---- S和domain的大小相同，使用S的值作为domain值的附加偏移量
B=ordfilt2(... , padopt) ---- 控制矩阵边界扩展的方式，若padopt设置为默认值zeros，在边界用0扩展；若padopt设置为symmetric，则使用对称法扩展边界。
参数domain相当于二值图像处理的结构方式，在数组中只包含0和1值，1值对应定义了滤波的邻域。示例：
B=ordfilt2(A, 5, ones(3, 3))      %执行3x3中值滤波器
B=ordfilt2(A, 1, ones(3, 3))      %执行3x3最小值滤波器
B=ordfilt2(A, 9, ones(3, 3))      %执行3x3最大值滤波器
B=ordfilt2(A, 1, [0 1 0;1 0 1;0 1 0])      %通过东西南北邻值来置换矩阵A的每一个元素
参数S被用于灰度形态学操作，包括灰度膨胀和腐蚀。

3）锐化滤波器：
⑴ 微分法：
梯度是图像处理常用的一次微分方法，梯度幅度比例于相邻像素的灰度级差值。在灰度骤变区域，梯度值大；在灰度相似区域，梯度值小；在灰度级为常数的区域，梯度为零。
Laplacian算子是线性二次微分算子，具有旋转不变性，从而满足不同走向的图像边界的锐化要求。Laplacian算子锐化后的图像，在灰度均匀区间或灰度斜坡部分为0，在灰度斜坡的顶点和底部均不为0，在底部形成灰度级的下冲，在顶部形成灰度级的上冲；灰度级界限的低灰度级一侧形成灰度级下冲，而在界限的高灰度级一侧形成灰度级的上冲。正是这些下冲和上冲的存在，勾画出图像区域的边缘轮廓，对边缘检测有很好的功效。
⑵ 模板匹配法：
事先准备好8个方向大小3x3的模板，锐化时顺序作用于同一图像窗口，对每一个模板，将窗口内各像素灰度值分别乘以该模块对应的数组元素，对积求和，将和SUM排序，最大SUM的值就是锐化输出的灰度值，这种锐化法就是模板匹配法。
典型的空间域边缘检出模板有：罗比逊Robinson模板、普雷外特Prewitt模板、柯赤kirsch模板。模板匹配法除了能增强图像边缘外，还具有平滑噪声的优点。
锐化图像时，使用fspecial函数的laplacian或prewitt参数获得相应的滤波器算子，然后使用filter2函数，使用前面得到的相应算子。

3. 频域增强：

在频域内也可以进行滤波和边缘增强，前者采用低通滤波器，后者一般使用高通滤波器。
1）低通滤波器：
一幅图像的边缘、跳跃部分以及颗粒噪声代表图像信号的高频分量，而大面积的背景区域代表了图像信号的低频分量。低通滤波器的作用就是滤除这些高频分量，保留低频分量，使图像信号平滑。常用的低通滤波器有几种：
⑴ 理想低通滤波器：
理论上低通频段无损通过，而区域外的高频信号被滤除。如果高频信号含有大量边缘信息，则也会被滤除，将会发生图像模糊现象。
⑵ 巴特沃斯Butterworth低通滤波器：
由于在通带与阻带间有个平滑的过渡带存在，高频信号并没有完全滤除，因此边缘模糊程度大大降低。
⑶ 指数低通和梯形低通滤波器等：
2）高通滤波器：
高通滤波器让高频信号通过，抑制低频信号。其传递函数主要有理想高通滤波器、巴特沃斯高通滤波器、指数高通滤波器、梯形高通滤波器等。
3）同态滤波器：
把频率过滤和灰度变换结合起来的图像处理方法称同态滤波，它是把图像的照明反射模型作为频率处理的基础，利用压缩亮度范围和增强对比度来改善图像的一种处理方法。

4. 色彩增强：

人对灰度级只能分辨出大于二十几种，但却能识别成千上万的色彩。色彩的增强主要分为真彩色增强和伪彩色增强。

1）真彩色增强：
把真实反映自然物体本来颜色的图像称为真彩色图像。真彩色增强主要分为4个方法：
·分别获取红、绿、蓝图像，可以称为单色提取增强
·把一幅真彩色图像分成红、绿、蓝三幅图像，然后再进行单色增强处理
·真彩色图像的退色处理
·把真彩色图像转换成HSV图像模型（或其他模型），再针对颜色模型分量进行增强处理

2）伪彩色增强：
由于人眼对彩色的分辨能力远远大于灰度分辨力，伪彩色增强的目的是增强观察者对图像信息的检测能力。主要方法是将二维数据阵列通过一个映射关系转换到真彩色图像平面上。
⑴ 灰度分割增强：
灰度分割即使用多分层技术，经等密度分层，然后分配颜色。
⑵ 滤波处理：
滤波处理的方法是把灰度级转换到频域，针对不同的频率进行颜色增强。典型的滤波处理是使用低通、带通和高通滤波器以得到三个范围的频率分量，分别计算出相应的R、G、B亮度值。
⑶ 灰度转换成彩色：
灰度图像转换成彩色图像，从技术上称为灰度图像的伪彩色处理。灰度分割是其中一种比较简单的方法，而滤波处理是频域处理的方法，具体的方法很多。通常方法是把灰度图像上的每一个像素点送人三个通道经过实施不同的变换得到R、G、B的亮度值。

四、图像复原：

图像复原是早期图像处理的主要内容之一，目的在于消除或减轻在图像获取及传输过程中造成的图像品质下降，恢复图像的本来面目。图像退化的典型表现是图像出现模糊、失真及出现加性噪声等为了更好地显示出图像原有的面貌，必须对图像进行必要的处理，复原出原始图像的本色效果。
退化的主要原因有：摄像机在捕捉图像过程的移动或长时间图像的曝光，远距离焦距、宽角度镜头、大气的存在物的影响或由于曝光比较短而使得捕捉的光子量少，光学系统离散的几何畸变，图像远距离的传输产生加性的噪声，图片的保存不当引起纸质的变换等。
图像复原的代数方法有非约束复原方法和约束复原方法，差别是附加某种约束条件，具体实现有逆滤波复原和最小二乘法复原等方法，最小二乘法也就是维纳滤波。

1. 棋盘图形函数checkerboard：
I=checkerboard ---- 创建一个8x8的正方形棋盘格图像，每个正方形包含10个像素点。
I=checkerboard(N) ---- 指定正方形每边的像素点为N个
I=checkerboard(N, P, Q) ---- 创建一个指定行数P和指定列数Q的矩形棋盘，每一片报告4个正方形，每边N个像素点。Q默认值为P。

2. 维纳滤波复原：
对图像进行维纳复原使用deconvwnr函数。调用格式：
J=deconvwnr(I, PSF) ---- 复原PSF和可能的加性噪声卷积退化的图像I。算法是基于最佳的估计图像和真实图像的最小均方差误差，和噪声图像的相关运算。在没有噪声的情况下，维纳滤波就是理想逆滤波。
J=deconvwnr(I, PSF, NSR) ---- NSR是噪信功率比，可以是标量或与I相同大小的数组，缺省0
J=deconvwnr(I, PSF, NCORR, ICORR) ---- NCORR和ICORR分别是噪声和原始图像自相关函数。NCORR和ICORR是不大于原始图像大小或维数，一个N维NCORR或ICORR数组是对应于每一维的自相关。若PSF为向量，NCORR或ICORR向量表示第一维的自相关函数；若PSF是数组，PSF的所有非单维对称推断一维自相关函数。
输出图像J能够展示算法中的离散傅里叶变换而产生的振铃，在处理图像调用deconvwnr之前，先调用edgetaper函数，可以减少振铃。

3. 规则化滤波复原：
对图像进行规则化滤波复原用deconvreg函数，规则化滤波对有限的加性噪声十分有效。
J=deconvreg(I, PSF) ---- 复原可能的加性噪声和PSF相关退化的图像I。在保持图像的平滑的情况下，算法是估计图像和实际图像间最小二乘法误差最佳约束。
J=deconvreg(I, PSF, NOISEPOWER) ---- NOISEPOWER是加性噪声功率，缺省值0
J=deconvreg(I, PSF, NOISEPOWER, LRANGE) ---- LRANGE向量是寻找最佳解决定义值范围。运算法则就是在LRANGE范围内找到一个最佳的拉格朗日乘数。如果LRANGE是标量，算法的LAGRA假定给定并等于LRANGE，NP值被忽略。缺省的范围是[1e-9 1e9]。
J=deconvreg(I, PSF, NOISEPOWER, LRANGE, REGOP) ---- REGOP是约束自相关的规则化算子。保持图像平滑度的缺省规则化算子是Laplacian算子。REGOP数组的维数不能超过图像的维数，任何非单独维与PSF的非单独维相对应。
[J, LAGRA]=deconvreg(I, PSF, ...) ---- 输出拉格朗日乘数值LAGRA，并且复原图像。
输出图像J能够出现算法中的离散傅里叶变换而产生的振铃。在处理图像调用drconvwnr之前，先调用edgetaper函数，可以减少振铃。

4. Lucy-Richardson复原：
对图像进行Lucy-Richardson复原用deconvlucy函数。调用格式：
J=deconvlucy(I, PSF) ---- 复原由可能的加性噪声和PSF相关退化的图像I。算法是基于结果图像J的似然最大值，它是在泊松统计下原始图像I的一个实例。输入行列I是数字行列或胞行列。为了改善复原效果，deconvlucy函数支持几个可选择的参数，如果没有定义用[]标识。
J=deconvlucy(I, PSF, NUMIT) ---- 定义了deconvlucy函数重复执行的次数，如果值没有指定，缺省值为10。
J=deconvlucy(I, PSF, NUMIT, DAMPAR) ---- DAMPAR定义了结果图像的偏差阈值
J=deconvlucy(I, PSF, NUMIT, DAMPAR, READOUT) ---- 定义相应加性噪声值和读出相机噪声值
J=deconvlucy(I, PSF, NUMIT, DAMPAR, READOUT, WEIGHT) ---- WEIGHT定义了指定每个像素反映相机记录质量的分量
deconvlucy(I, PSF, NUMIT, DAMPAR, READOUT, WEIGHT, SUBSMPL) ---- SUBSMPL而二次抽样，缺省值为1
输出图像J能够出现算法中的离散傅里叶变换而产生的振铃。在处理图像调用deconvwnr之前，先调用edgetaper函数，可以减少振铃。比如：I=edgetaper(I, PSF)。

5. 盲去卷积复原：
盲去卷积复原是利用原始模糊图像，估算PSF和清晰图像的一种图像复原方法。对图像进行盲去卷积运算复原用deconvblind函数。调用格式：
[J, PSF]=deconvblind(I, INITPSF) ---- 对图像I进行最大似然法则返回复原图像J和复原的点扩展函数PSF。
[J, PSF]=deconvblind(I, INITPSF, NUMIT) ---- NUMIT指定了反复的次数，缺省为10
[J, PSF]=deconvblind(I, INITPSF, NUMIT, DAMPAR) ---- DAMPAR定义了结果图像的偏差阈值
[J, PSF]=deconvblind(I, INITPSF, NUMIT, DAMPAR, WEIGHT) ---- WEIGHT指定了输入图像哪些像素被复原采纳
[J, PSF]=deconvblind(I, INITPSF, NUMIT, DAMPAR, WEIGHT, READOUT) ---- READOUT定义了相应的加性噪声值和读出相机噪声值，缺省为0
[J, PSF]=deconvblind(... , FUN, P1, P2, ... , PN) ---- FUN是描述PSF的加性约束函数
有四种方法定义了FUN：函数句柄，内联对象，包含函数名的字符串，包含MATLAB表达式的字符串。

6. 图像复原的其他函数：
⑴ edgetaper函数：退化输入图像边缘
J=edgetaper(I, PSF)
用输入点扩散函数PSF来退化（模糊）输入图像的边缘I，输出图像是原始图像I和其模糊图像的加权和。加权数组由PSF函数的自相关决定，在中间区域J等于I，而在边缘区域等于退化的状态。
edgetaper函数能够有效地减少由于用离散傅里叶变换退化方法而产生的振铃现象。
⑵ psf2otf函数：把点扩散函数转换成光传递函数
OTF=psf2otf(PSF) ---- 计算点扩展函数PSF的快速傅里叶变换并创建光传递函数数组
OTF=psf2otf(PSF, OUTSIZE)
OTF不被PSF中心影响，缺省OTF数组和PSF大小一致。
⑶ otf2psf函数：把光传递函数转换成点扩展函数
PSF=otf2psf(OTF)
PSF=otf2psf(OTF, OUTSIZE) ---- 指定输出数组的大小OUTSIZE
通过计算光传递函数OTF数组的逆快速傅里叶变换，在起始位置上创建点扩展函数PSF。缺省PSF和OTF的大小相等。输出数组在任何维都不能超过OTF的大小。

五、图像分析：

图像分析就是对图像进行描述，即用一组数或符号表征图像中目标区的特征、性质和相互关系，为模式识别提供基础。描述一般是针对图像或景物中的特定区域或目标。为了描述，首先要进行分割，边缘检测是图像分割所依赖的重要特征。

1. 阈值分割：

图像分割就是将图像中有意义的特征区域或者需要应用的特征区域提取出来，这些特征区域可以是像素的灰度值、物体轮廓曲线、纹理特性等，也可以是空间频谱或直方图特征等。
阈值分割是一种简单有效的图像分割方法，它对物体与背景有较强对比的图像分割特别有效，所有灰度大于或等于阈值的像素被判决为属于物体，灰度值用255表示前景，否则这些像素点被排除在物体区域以外；灰度值为0表示背景。多阈值分割只是分割技巧问题，与单阈值分割没有本质区别。
1）双峰法：
双峰法的原理很简单，它认为图像由前景和背景两部分组成，图像的灰度分布曲线近似是由两个状态分布函数叠加而成，图像的直方图将会出现两个分离的峰值。双峰之间的波谷出就是图像的阈值所在。一般要使用imhist和im2bw函数。
将原始图像和阈值分割后的图像比较，可以发现有些前景图像和背景图像的灰度值太接近，导致有些前景图像没有从背景分离出来。
2）迭代法：
迭代法阈值选择算法是对双峰法的改进，它首先选择一个近似阈值T，将图像分割成两部分R1和R2，计算区域R1和R2的均值u1和u2，选择新的分割阈值T=(u1+u2)/2，重复上述步骤，直到u1和u2不再变换为止。
迭代法基于逼近的思想，步骤为：
·求出图像的最大灰度值ZMAX和最小灰度值ZMIN，令阈值T0=(ZMAX+ZMIN)/2
·根据阈值T将图像分割为前景和背景，分别求出二者的平均灰度值ZO和ZB
·求出新阈值T=(ZO+ZB)/2
·若两个平均灰度值ZO和ZB不再变换，或T不再变化，则T为阈值
对于uint8类型，计算容易取整，使得迭代次数有限；若为double类型图像，则可以取一个允许的误差值，只要迭代变化小于这个误差值就认为迭代结束，防止无限次迭代。
迭代所得的阈值分割图像效果良好，比双峰法分割效果有很大提高，但在图像的细微处还没有很好区分。对某些特定的图像，微小数据的变化会引起分割效果的巨大改变。
3）大津法：
大津法ITSU是由大津1979年提出。对图像I，T为前景与背景的分割阈值，前景点数占图像比例为w0，平均灰度u0；背景点数占图像比例为w1，平均灰度u1。图像的总平均灰度为ut=w0xu0+w1xu1。从最小灰度值到最大灰度值遍历T，当T使得方差值最大时，T即为分割的最佳阈值。方差是灰度分布均匀性的一种度量，方差值越大，说明构成图像的两部分差别越大，当部分前景错分为背景或部分背景错分为前景都会导致两部分差别变小，因此使方差最大的分割意味着错分概率最小。方差计算公式为：

直接使用大津法计算量较大，实现时一般采用等价的公式：

MATLAB中，graythresh函数用大津法计算全局图像的阈值。
大津法选取出来的阈值非常理想，对各种情况的表现都较为良好，虽然很多情况下都不是最佳分割，但分割质量通常都有一定的保障，可以说是最稳定的分割。

2. 边缘检测：

两个具有不同灰度值的相邻区域之间总存在边缘，边缘是灰度不连续的表现。常见的边缘点有阶梯边缘Step-edge、屋顶边缘Roof-edge、线性边缘Line-edge。
由于边缘是图像上灰度变化最剧烈的地方，传统的边缘检测就是利用了这个特点，对图像的各个像素点进行微分或求二阶微分来确定边缘像素点。一阶微分图像的峰值处对应图像的边缘点；二阶微分图像的过零点处对应图像的边缘点。根据数字图像的特点，处理图像过程中常采用差分来替代导数运算。对于图像的简单一阶导数运算，由于具有固定的方向性，只能检测特定方向的边缘，不具有普遍性。为了克服一阶导数的缺点，采用图像的梯度算子，它是图像处理中最常用的一阶微分算法。图像梯度的最重要性质是梯度的方向是在图像灰度最大变化率上，恰好可以反映出图像边缘上的灰度变换。
图像边缘提取的常用算子有Robert算子、Sobel算子、Prewitt算子、拉普拉斯算子等。MATLAB中使用edge函数实现边缘检测的功能。
1）微分算子Roberts、Sobel、Prewitt。
Roberts模板为2x2，有两种。Sobel和Prewitt模板为3x3，也都有两种。
BW=edge(I, 'sobel') ---- 使用Sobel算子自动选择阈值进行边缘检测
BW=edge(I, 'sobel', thresh) ---- 根据指定的敏感阈值thresh边缘检测，忽略小于阈值的阈值
BW=edge(I, 'sobel', thresh, direction) ---- 边缘检测方向，可选值horizontal、vertical、both
[BW, thresh]=edge(I, 'sobel', ...) ---- 返回阈值thresh和边缘检测图像BW

BW=edge(I, 'prewitt') ---- 使用Prewitt算子自动选择阈值进行边缘检测
BW=edge(I, 'prewitt', thresh)
BW=edge(I, 'prewitt', thresh, direction)
[BW, thresh]=edge(I, 'prewitt', ...)

BW=edge(I, 'roberts') ---- 用Roberts算子自动选择阈值进行边缘检测
BW=edge(I, 'roberts', thresh) ---- 根据指定的敏感阈值thresh
[BW, thresh]=edge(I, 'roberts', ...) ---- 返回阈值thresh和边缘检测图像BW
2）Log算子：
拉普拉斯算子是一种二阶边缘检测算子，是线性的、移不变的算子。由于图像经二阶微分后，在边缘处产生一个陡峭的过零点，根据这个过零点进行判断边缘。
图像边缘的一阶微分是极值点，二阶微分为零，确定过零点的位置要比确定极值点容易且精确。但二阶微分对噪声更敏感，因此在对图像进行拉普拉斯算子进行边缘检测前，一般先对图像平滑滤波，多采用高斯滤波器。把高斯平滑滤波和拉普拉斯锐化滤波器结合起来，先平滑噪声，再进行边缘检测，这种方法称为高斯拉普拉斯算子，简写Log。常用的算子是5x5的模块。在Log算子中对边缘判断采用的技术是过零Zero-crossing检测。
BW=edge(I, 'log') ---- 用Log算子自动选择阈值进行边缘检测
BW=edge(I, 'log', thresh) ---- 根据选择的阈值thresh检测，忽略小于阈值的边缘
BW=edge(I, 'log', thresh, sigma) ---- 参数sigma指定Log滤波器标准偏差，缺省值2，滤波器为nxn，这里n=ceil(sigma*3)*2+1。
[BW, threshold]=edge(I, 'log', ...) ---- 返回阈值thresh和边缘检测图像BW

BW=edge(I, 'zerocross', thresh, h) ---- 用滤波器h指定过零检测法，thresh为阈值
[BW, thresh]=edge(I, 'zerocross', ...) ---- 返回阈值thresh和边缘检测图像BW
3）Canny算子：
Canny算子是寻找图像梯度的局部最大值。一个阈值的判断往往不够，由于噪声影响造成斑纹现象Steaking，也就是边缘是断的。如果降低阈值，又会发现错误的边缘。Canny提出了双阈值方法。
滤波器尺度在离散情形下就是指模板的宽度W，W越大检测出的边缘效果越好，噪声影响越小，但定位越不准确。为了解决这个矛盾，Canny提出了多尺度控件边缘检测。
Canny算子的步骤为：
·首先用二维高斯滤波模板对图像进行滤波以消除噪声
·用导数算子（如Prewitt、Sobel）找到图像灰度的沿着两个方向的偏导数，并求出梯度的大小和方向
·把边缘的梯度方向大致地分为四种（水平、垂直、45度方向、135度方向），各个方向用不同的邻近像素进行比较，以决定极大值。若某个像素的灰度值与其梯度方向上前后两个像素的灰度值相比不是最大的，则这个像素值置为0，即不是边缘，这个过程称非极大值抑制。
·使用累计直方图计算两个阈值。凡是大于高阈值的一定是边缘，凡是小于低阈值的一定不是边缘；如果检测结果大于低阈值但又小于高阈值，那么就要看这个像素的邻接像素中有没有超过高阈值的边缘像素，如果有那么就是边缘，否则就不是边缘。
BW=edge(I, 'canny') ---- 用Canny算子自动选择阈值进行边缘检测
BW=edge(I, 'canny', thresh) ---- 根据给定阈值thresh进行边缘检测，参数thresh为二元向量，第1个元素为低阈值，第2个元素为高阈值；如果thresh为标量，则此值为高阈值，0.4*thresh被用作低阈值。
BW=edge(I, 'canny', thresh, sigma) ---- 指定阈值和高斯滤波器的标准偏差sigma，缺省为1
[BW, threshold]=edge(I, 'canny', ...) ---- 返回二元阈值和图像BW

3. 四叉树分解：

四叉树分解是一种基于均匀性检测的图像分割方法。四叉树要求图像大小N为2的幂，NxN大小的图像f数据结构是一个1x1到NxN逐次增加的n+1个图像构成的序列。序列中1x1图像是f所有像素灰度的平均值构成的图像；序列2x2图像将图像f划成4个大小相同且互不重叠的正方形区域，各区域的像素灰度平均值分别作为2x2图像相应位置上的四个像素灰度；对于已经划分的4个区域分别再一次一分为四，然后求各区域的灰度平均值作为4x4图像的像素灰度；重复这个过程，直至图像尺寸变为NxN为止。上面的四叉树结构也可以从相反的方向来构造，首先从NxN入手，分成N/2 x N/2大小相同互不重叠的区域，然后逐渐分割。这一结构可以用树结构表示，树的根节点对应于整个图像，它的叶子对应图像的像素，每个节点有4个叉枝，从而称为图像的四叉树。
图像四叉树分解过程为：将NxN原始图像分成四个相同大小的区域，判断每个区域是否符合一致性标准，如果符合一致性标准，则停止分割图像，如果不符合一致性标准，则继续分割图像，并且把每次分割后的区域进行一致性判断，直到分割成图像中所有区域都符合一致性标准为止。所谓一致性标准，通常指区域内各像素点的灰度范围不超过某个阈值，也就是各像素点的灰度值的接近程度满足要求。
1）qtdecomp函数：实现四叉树分解
S=qtdecomp(I) ---- 对灰度图像I执行四叉树分解，返回一个四叉树结构S，S是稀疏矩阵。若(k, m)非零，那么像素点(k, m)为分解结构中一个子图像块的左上顶点，而这个图像块的大小由(k, m)给定。缺省情况下，qtdecomp函数分割图像块直到所有的图像块中的像素点符合指定的阈值为止。
S=qtdecomp(I, threshold) ---- 分割图像直到块中元素的最大值和最小值不大于threshold。参数threshold的范围[0 1]。若I为uint8类型，把阈值乘以255作为实际的阈值使用；若I为uint16，把阈值乘以65535作为实际阈值使用。
S=qtdecomp(I, threshold, mindim) ---- 将不产生小于mindim的图像块
S=qtdecomp(I, threshold, [mindim maxdim]) ---- 将不产生比mindim小比maxdim大的图像块。mindim/maxdim必须为2的整数次幂。
S=qtdecomp(I, fun) ---- fun函数确定是否分割图像块，fun函数应该返回只取0和1元素的k维向量，其中1表示关联的块继续分割，而0表示不再分割。fun函数可以是一个函数句柄，由@创建，或者内联函数。
S=qtdecomp(I, fun, P1, P2, ...) ---- 把P1、P2等作为附加参量传递给fun函数。
2）qtgetblk函数：获取四叉树分解后的图像块值
[vals, r, c]=qtgetblk(I, S, dim) ---- 返回图像I的四叉树分解中dimXdim图像块的矩阵vals，其中参数S为qtdecomp函数返回的包含四叉树结构的稀疏矩阵，参数vals为一个dimXdimXk的矩阵，这里k为四叉树分解中dimXdim块的数量。若四叉树分解结构中没有定义大小的块输出值为空矩阵。参数r和c包含了块左上角的行坐标和列坐标的向量。
[vals, idx]=qtgetblk(I, S, dim) ---- 返回图像块的左上角的线性索引idx
3）qtsetblk函数：设置四叉树分解中子块的值
J=qtsetblk(I, S, dim, vals)
置换图像I四叉树分解中所有dimXdim子块为由vals构成的dimXdim子块。参数S为qtdecomp函数返回的包含四叉树结构的稀疏矩阵，参数vals为一个dimXdimXk的矩阵，这里k为四叉树分解中dimXdim块的数量。

六、图像压缩：