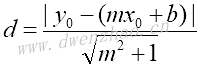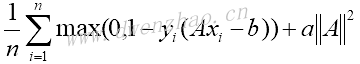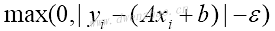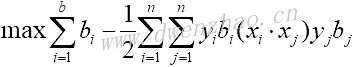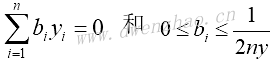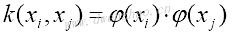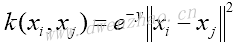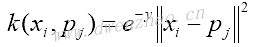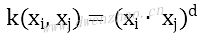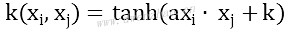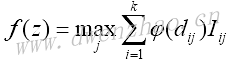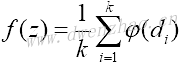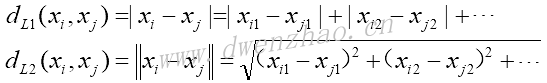TensorFlow机器学习

TensorFlow支持Linux、macOS和Window操作系统，虽然是使用C++编写，但更常用Python等语言编程。虽然TensorFlow可在CPU上运行，但大多数算法在GPU上运行会更快，支持英伟达Nvidia显卡，常用的是Nvidia Tesla和Nvidia Pascal，至少需要4GB的视频RAM，为此需要下载Nvidia Cuda Toolkit v5.x以上版本，还常使用Scipy、Numpy、Scikit-Learn等Python第三方库，这些都在Anaconda软件包中。
使用TensorFlow之前，需要导入，一般使用：
import tensorflow as tf

1）使用TesnsorFlow算法的一般流程：

  ·  导入/生成样本数据集：所有机器学习算法都依赖样本数据集，可使用生成的样本数据集，也可以使用外部公开的样本数据集
  ·  转换和归一化数据：输入的样本数据集一般并不符合TensorFlow期望的格式，需要在使用前进行相应转换，大部分机器学习算法希望输入的样本数据是归一化的数据，TensorFlow有内建的函数实现归一化，如tf.nn.batch_norm_with_global_normalization()
  ·  划分训练样本数据集和验证样本数据集：一般情况下，要求机器学习算法的训练数据集和测试数据集不同，还有一些算法要求超参数调优，因此需要验证样本集来决定最优的超参数
  ·  设置机器学习参数：机器学习经常需要一系列的常量参数，如迭代次数、学习率等，一般是一次性初始化所有的机器学习参数
  ·  初始化变量和占位符：在求解最优化过程中，TensorFlow通过占位符传入数据，并调整变量，如权重、偏差。TensorFlow指定数据大小和数据类型来初始化变量和占位符
  ·  定义模型结构：TensorFlow通过选择操作、变量、占位符的值来构建计算图
  ·  声明损失函数：损失函数能说明预测值与实际值的差距，用来评估输出结果
  ·  初始化模型和训练模型：TensorFlow创建计算图实例，通过占位符传入数据，维护变量的状态信息
  ·  评估机器学习模型：需要一种标准评估机器学习模型对样本数据集的效果，通过评估可以确定机器学习模型是过拟合还是欠拟合
  ·  调优超参数：大部分情况下需要基于模型效果来调整一些超参数，通过调整不同的超参数来重复训练模型，并用验证样本集来评估机器学习模型
  ·  发布/预测结果：机器学习模型一旦训练好，最后都用来预测新的未知的数据

2）声明变量和张量：

TensorFlow的主要数据结构是张量tensor，用张量来操作计算图。在TensorFlow中，可以把变量或占位符声明为张量。不过，在TensorFlow中创建一个张量，并不会在计算图中增加内容，只有运行一个操作来初始化变量后，TensorFlow才会把此张量增加到计算图。
⑴ 固定张量：
  ·  创建指定维度的零张量：
  zeros_tsr=tf.zeros([row_dim, col_dim])
  ·  创建指定维度的全1张量：
  ones_tsr=tf.ones([row_dim, col_dim])
  ·  创建指定维度的常数填充的张量：
  filled_tsr=tf.fill([row_dim, col_dim], 42)
  ·  用已知参数张量创建一个张量：
  constant_tsr=tf.constant([1, 2, 3])
tf.constant()函数也能广播一个值为数组，然后模拟tf.fill()函数的功能，方法为tf.constant(42，[row_dim, col_dim])。
⑵ 相似形状的张量：
新建一个与给定的tensor一致的tensor，其所有元素为0或为1，方式为：
  zeros_similar=tf.zeros_like(constant_tsr)   ones_similar=tf.ones_like(constant_tsr)
因为这样声明的张量依赖于前面的张量，因此初始化时需要按序进行，不能一次性初始化。
⑶ 序列张量：
TensorFlow可以创建指定间隔的张量，输出与numpy包的range()函数和linspace()函数的输出一致：
  linear_tsr=tf.linspace(start=0, stop=1, start=3)   # 返回张量[0.0, 0.5, 1.0]   integer_seq_tsr=tf.range(start=6, limit=15, delta=3)   # 返回张量[6, 9, 12]，不包括limit
⑷ 随机张量：
  ·  使用tf.random_uniform()函数生成均匀分布的随机数：
  randunif_tsr=tf.random_uniform([row_dim, col_dim], minval=0, maxval=1)
随机分布范围为[minval, maxval)，包括minval，不包括maxval。
  ·  使用tf.random_normal()函数生成正态分布的随机数：
  randnorm_tsr=tf.random_normal([row_dim, col_dim], mean=0.0, stddev=1.0)
  ·  使用tf.truncated_normal()函数生成带有指定边界的正态分布的随机数：
  runcnorm_tsr=tf.truncated_normal([row_dim, col_dim], mean=0.0, stddev=1.0)
随机数位于指定期望值到两个标准差之间的区间。
  ·  函数tf.random_shuffle()和tf.random_crop()使张量/数组的随机化：
  shuffled_output=tf.random_shuffle(input_tensor)   cropped_output=tf.random_crop(input_tensor, crop_size)
  ·  使用tf.random_crop()函数对张量指定大小的随机剪裁：
  cropped_image=tf.random_crop(my_image, [height/2, width/2, 3])
上面代码对3通道颜色图像进行随机剪裁，为了固定剪裁结果的一个维度，需要在相应维度上赋其最大值。
⑸ 封装张量作为变量：
  my_var=tf.Variable(tf.zeros([row_dim, col_dim]))
创建张量tensor未必要用TensorFlow内建函数，也可以使用tf.convert_to_tensor()函数将任意numpy数组转换为Python列表，或者将常量转换为一个张量。此函数也可以接受张量为输入。

3）使用占位符和变量：

使用数据的关键点之一要清楚它是占位符还是变量。变量是TensorFlow算法的参数，TensorFlow维护这些变量的状态来优化算法；占位符是TensorFlow对象，用于表示输入/输出数据的格式，允许传入指定类型和形状的数据，并依赖计算图的计算结果。
⑴ 变量：
在TensorFlow中，使用函数tf.Variable()创建变量，输入一个张量返回一个变量。声明一个变量后需要初始化，也就是将变量与计算图相关联。示例：
  my_var=tf.Variable(tf.zeros([2, 3]))   sess=tf.Session()   initialize_op=tf.global_variables_initializer()   sess.run(initialize_op)
上述代码创建变量并初始化。
⑵ 占位符：
占位符仅仅声明数据位置，用于传入数据到计算图。占位符通过会话中的feed_dict参数获取数据。在计算图中使用占位符时，必须在其上执行至少一个操作。示例：
  sess=tf.Session()   x=tf.placeholder(tf.float32, shape=[2, 2])   y=tf.identity(x)   x_vals=np.random.rand(2, 2)   sess.run(y, feed_dict={x: x_vals})
上述代码中，初始化计算图，声明一个占位符x，定义y为x的identity操作，用于返回占位符传入的数据本身。上面示例中，计算图只有一个变量且全部初始化为0。TensorFlow不会返回一个自相关的占位符，即运行sess.run(x, feed_dict={x: x_vals})将会报错。
在计算图运行过程中，需要告知TensorFlow初始化所创建的变量时机。TensorFlow中每个变量都有initializer方法，但最常用的是辅助函数global_variables_initializer()，此函数会一次性初始化所创建的所有变量，使用方式为：
  initialize_op=tf.global_variables_initializer()
但是，如果是基于已经初始化的变量进行初始化，就必须按序进行，方式为：
  sess=tf.Session()   first_var=tf.Variable(tf.zeros([2, 3]))   sess.run(first_var.initializer)   second_var=tf.Variable(tf.zeros_like(first_var))   sess.run(second_var.initializer)

4）操作矩阵：

在机器学习中，矩阵是很重要的概念，大多数机器学习算法是基于矩阵运算的。在TensorFlow中，矩阵计算相当容易。
⑴ 创建矩阵：
可以使用numpy数组创建二维矩阵，也可以使用创建张量的函数并为其指定一个二维形状来创建矩阵，还可以使用diag()函数从一个一维数组或列表创建对角矩阵：
  import tensorflow as tf   sess=tf.Session()   identity_matrix=tf.diag([1.0, 1.0, 1.0])   A=tf.truncated_normal([2, 3])   B=tf.fill([2, 3], 5.0)   C=tf.random_uniform([3, 2])   D=tf.convert_to_temsor(np.array([[1., 2., 3.], [-3., -7., -1.], [0., 5., -2.]]))   print(sess.run(identity_matrix))   print(sess.run(A))   print(sess.run(B))   print(sess.run(C))   print(sess.run(D))
⑵ 矩阵的加法、减法和乘法：
  print(sess.run(A+B))   print(sess.run(B-B))   print(sess.run(tf.matmul(B, identity_matrix)))
矩阵乘法函数tf.matmul()可以通过参数指定在操作前是否进行转置或是否每个矩阵都是稀疏的。
⑶ 矩阵转置：
  print(sess.run(tf.transpose(C)))
⑷ 矩阵行列式：
  print(sess.run(tf.matrix_determinant(D)))
⑸ 矩阵的逆矩阵：
  print(sess.run(tf.matrix_inverse(D)))
TensorFlow在矩阵求逆使用Cholesky矩阵分解法，也称平方根法，矩阵需要为对称正定矩阵或者可进行LU分解。
⑹ 矩阵分解：
使用Cholesky矩阵分解法：
  print(sess.run(tf.cholesky(identity_matrix)))
⑺ 矩阵的特征值和特征向量：
  print(sess.run(tf.self_adjoint_eig(D)))
输出结果中，第一行为特征值，剩下的向量是对应的特征向量，这种方法也称为矩阵的特征分解。

5）张量的基本操作及数学函数：

TensorFlow中张量的基本操作有add()、sub()、mul()、div()，是对张量的每个元素进行操作。
⑴ div()函数：有多种形式，其返回值的数据类型与输入数据类型一致
  print(sess.run(tf.div(3, 4)))   # 0
⑵ truediv()函数：在除法操作前强制转换整数为浮点数，最终结果为浮点数
  print(sess.run(tf.truediv(3, 4)))   # 0.75
⑶ floordiv()函数：返回浮点数结果，但会向下舍去小数位到最近的整数
  print(sess.run(tf.floordiv(3.0, 4.0)))   # 0.0
⑷ mod()函数：返回除法的余数
  print(sess.run(tf.floordiv(22.0, 5.0)))   # 2.0
⑸ cross()函数：计算两个张量的叉积，只为三维向量定义
  print(sess.run(tf.cross([1.0, 0.0, 0.0], [0., 1., 0.])))   # [0. 0. 1.0]
⑹ 自定义函数：
  def custom_polynomial(value):      return tf.sub(3*tf.square(value), value)+10   print(sess.run(custom_polynomial(11)))   # 362
上述代码定义了一个二次多项式函数3x²-x+10。
⑺ 数学函数列表：

abs()	返回输入参数张量的绝对值
ceil()	返回输入参数张量的向上取整结果
cos()	返回输入参数张量的余弦值
exp()	返回输入参数张量的自然常数e的指数
floor()	返回输入参数张量的向下取整结果
inv()	返回输入参数张量的倒数
log()	返回输入参数张量的自然对数
maximum()	返回两个输入参数中元素的最大值
minimum()	返回两个输入参数中元素的最小值
neg()	返回输入参数张量的负值
pow()	返回输入参数第一个张量的第二个张量的次幂
round()	返回输入参数张量的四舍五入结果
rsqrt()	返回输入参数张量的平方根的倒数
sign()	返回输入参数张量的符号，返回-1、0或1
sin()	返回输入参数张量的正弦值
sqrt()	返回输入参数张量的平方根
square()	返回输入参数张量的平方
tan()	返回输入参数张量的正切值

⑻ 特殊数学函数列表：用在机器学习中的一些数学函数

digamma()	普西函数Psi，lgamma()函数的导数
erf()	返回张量的高斯误差函数
erfc()	返回张量的互补误差函数
igamma()	返回下不完全伽马函数
igammac()	返回上不完全伽马函数
lbeta()	返回贝塔函数绝对值的自然对数
lgamma()	返回伽马函数绝对值的自然对数
squared_difference()	返回两个张量间差值的平方

6）激励函数：

激励函数是使用神经网络算法中必备的函数，在张量上进行非线性操作，目的是为了调节权重和偏差。TensorFlow的激励函数位于神经网络库nn。
⑴ ReLU函数：
整流线性单元ReLU(Rectifier Linear Unit)激励函数是神经网络最常用的非线性函数，其函数为max(0, x)，连续但不平滑。
  print(sess.run(tf.nn.relu([-3., 3., 10.])))   # [0. 3. 10.]
⑵ ReLU6函数：
为了抵消ReLU激励函数的线性增长部分，会在min()函数中嵌入max(0, x)，称为ReLU6，表示为min(max(0, x), 6)，是hard-sigmoid函数的变种，计算速度快，解决梯度消失。
  print(sess.run(tf.nn.relu6([-3., 3., 10.])))   # [0. 3. 6.]
⑶ sigmoid函数：
最常用的连续且平滑的激励函数，也被称为逻辑函数(Logistic函数)，表示为1/(1+exp(-x))，取值范围0到1，不以0为中心，有些算法则要求优先使用均值为0的样本数据集。由于sigmoid函数在训练过程中反向传播项趋近于0，因此现在很少使用。
  print(sess.run(tf.nn.sigmoid([-1., 0., 1.])))   # [0.26894143 0.5 0.7310586]
⑷ tanh函数：
双曲正切函数tanh是双曲正弦与双曲余弦的比值，表示为((exp(x)-exp(-x))/((exp(x)+exp(-x)))，取值范围-1到1。
  print(sess.run(tf.nn.tanh([-1., 0., 1.])))   # [-0.76159418 0. 0.76159418]
⑸ softsign函数：
是符号函数的连续但不平滑估计，表达式x/(abs(x)+1)。
  print(sess.run(tf.nn.softsign([-1., 0., 1.])))   # [-0.5 0. 0.5]
⑹ softplus函数：
是ReLU函数的平滑版，表达式log(exp(x)+1)。
  print(sess.run(tf.nn.softplus([-1., 0., 1.])))   # [0.31326166 0.69314718 1.32326163]
⑺ ELU函数：
指数线性单元ELU(Exponential Linear Unit)，表达式(exp(x)+1) if x<0 else x。
  print(sess.run(tf.nn.elu([-1., 0., 1.])))   # [-0.63212055 0. 1.]
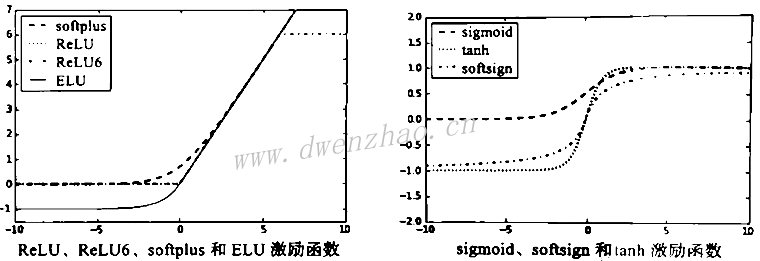
当输入无穷大时，softplus函数趋近于无穷大，ELU趋近于无穷大，softsign函数趋近于0；当输入无穷小时，softplus函数趋近于0，ELU趋近于-1，softsign函数趋近于-1。
⑻ 激励函数的选取：
激励函数是为计算图引入非线性部分，如果激励函数的取值范围在0到1之间，比如sigmoid函数，那样计算结果也只能在0到1之间选取。
如果激励函数隐藏在节点之间，要注意对传入张量的影响。如果张量要缩放为均值为0，就需要用激励函数以使得尽可能多的变量在0附近，要选用tanh函数或softsign函数；如果张量要缩放为正数，就应当选用保留变量在正数范围内的激励函数。
TensorFlow的激励函数
上图为激励函数的曲线，左侧4种激励函数ReLU、ReLU6、softplus、ELU，在函数输入值小于0时，输出值平直或逐渐变平；输入值大于0时，输出值线性增长（ReLU6有最大值6）。右侧3种激励函数sigmoid、tanh、softsign都是平滑的，具有类似S形，其中两个激励函数有水平渐近线。

7）读取数据源：

使用样本数据集训练机器学习算法模型，需要通过TensorFlow或Python访问各种数据源。有些数据使用Python内建库，有的需要编写Python脚本下载，也有的需要手动从网上下载，但都需要联网才能获取到。
⑴ 鸢尾花数据Iris data：
是机器学习和统计分析最经典的数据集，包括山鸢花、变色鸢尾和弗吉尼亚鸢尾各自的花萼和花瓣的长度和宽度，总共150个数据样本，每类有50个样本。
用Python加载样本数据集时，可以使用Scikit Learn数据集函数，方法为：
  from sklearn import datasets   iris=datasets.load_iris()   print(len(iris.data))   # 150   print(len(iris.target))   # 150   print(iris.data[0])   # Sepal length, Sepal width, Petal length, Petal width [5.1 3.5 1.4 0.2]   print(set(iris.target))   # I. setosa I. virginica I. versicolor {0, 1, 2}
⑵ 出生体重数据Birth weight data：
来自1986年斯普林菲尔德的Baystate医疗中心，是婴儿出生体重以及母亲和家庭历史人口统计医学指标，有189个样本集，包含11个特征变量。
使用Python访问数据方式：
  import requests   birthdata_url='http://github.com/nfmcclure/tensorflow_cookbook/raw/master       /01_Introduction/07_Working_with_Data_Sources/birthweight_daata/birthweight.dat'   birth_file=requests.get(birthdata_url)   birth_data=birth_file.text.split('\r\n')   birth_header=birth_data[0].split('\t')   birth_data=[[float(x) for x in y.split('\t') if len(x)>=1] for y in birth_data[1:] if len(y)>=1]   print(len(birth_data))   # 189   print(len(birth_data[0]))   # 9
⑶ 波士顿房价数据Boston Housing data：
此样本数据集保存在卡内基梅隆大学机器学习仓库，总共506个房价样本，包含14个特征变量。
使用Python获取数据方式：
  from keras.datasets import boston_housing   (x_train, y_train), (x_test, y_test)=boston_housing.load_data()   housing_header=['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',         'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']   print(x_train.shape[0])   # 404   print(x_train.shape[1])   # 13
⑷ MNIST手写体字库：
是NIST手写体字库的子样本数据集，下载网址http://yann.lecun.com/exdb/mnist/，包含70000张数字0到9的图片，其中60000张标注为训练样本数据集，10000张为测试样本数据集，常用于进行图像识别训练。
TensorFlow提供内建函数来访问MNIST数据集，从训练样本集中留出5000张图片作为验证样本数据集用来预防过拟合。使用Python访问数据方式：
  from tensorflow.examples.tutorials.mnist import input_data   mnist=input_data.read_data_sets("MNIST_data/", one_hot=True)   print(len(mnist.train.images))   # 55000   print(len(mnist.test.images))   # 10000   print(len(mnist.validation.images))   # 5000   print(mnist.train.labels[1,:])   # the first label is 3 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
⑸ 垃圾邮件文本数据Spam-ham text data：
访问数据方式：
  import requests   import io   from zipfile import ZipFile   zip_url='http://archive.ics.uci.edu/ml/machine-learning-databases/00228/sms/spamcollection.zip'   r=requests.get(zip_url)   z=ZipFile(io.BytesIO(r.content))   file=z.read('SMSSpamCollection')   text_data=file.decode()   text_data=text_data.encode('ascii', errors='ignore')   text_data=text_data.decode().split('\n')   text_data=[[x.split('\t') for x in text_data if len(x)>=1]   [text_data_target, text_data_train]=[list(x) for x in zip(*text_data)]   print(len(text_data_train))   # 5574   print(len(text_data_target))   # {'ham', 'spam'}   print(text_data_train[1])   # Ok lar... Joking wif u oni...
⑹ 影评样本数据：
是电影观看者的影评，分好评和差评，下载网址http://www.cs.cornell.edu/people/pabo/movie-review-data/。
Python数据处理方式：
  import requests   import io   import tarfile   movie_data_url='http://www.cs.cornell.edu/people/pabo/movie-review-data/rt-polarit/ydata.tar.gz'   r=requests.get(movie_data_url)   # Stream data into temp object   stream_data=io.BytesIO(r.content)   tmp=io.BytesIO()   while True:      s=stream_data.read(16384)      if not s:        break;      tmp.write(s)      stream_data.close()   tmp.seek(0)   # Extract tar file   tar_file=tarfile.open(fileobject=tmp, mode="r:gz")   pos=tar_file.extractfile('rt-polaritydata/rt-polarity.pos')   neg=tar_file.extractfile('rt-polaritydata/rt-polarity.neg')   # Save pos/neg reviews   pos_data=[]   for line in pos:      pos_data.append(line.decode('IOS-8859-1').encode('ascii', errors='ignore').decode())   neg_data=[]   for line in neg:      neg_data.append(line.decode('IOS-8859-1').encode('ascii', errors='ignore').decode())   tar_file.close()   print(len(pos_data))   # 5331   print(len(neg_data))   # 5331   # print out first negative review   print(neg_data[0])
⑺ CIFAR-10图像数据：
此图像数据集是CIFAR机构发布的8000万张彩色图片的子集，总共分为10类，60000张照片。50000张图片训练数据集，10000张图片测试数据集。访问地址http://www.cs.toronto.edu /~kriz/cifar.html。
⑻ 莎士比亚著作文本数据Shakespeare text data：
此文本数据集是古登堡数字电子书计划提供的免费电子书籍，其中编译了莎士比亚的所有著作。
用Python访问文本文件的方式：
  import requests   shakespeare_url='http://www.gutenberg.org/cache/epub/100.pg100.txt'   response=requests.get(shakespeare_url)   shakespeare_file=response.content   shakespeare_text=shakespeare_file.decode('utf-8')   shakespeare_text=shakespeare_text[7675:]   print(len(shakespeare_train))   # 5582212
⑼ 英德句子翻译数据：
此数据集由在线翻译数据库Tatoeba发布，ManyThings.org整理并提供下载，网址http://www. Manythings.org，提供英德语句互译的文本文件，也可以改变url获取需要的其他语言的文本文件。
Python使用方法：
  import requests   import io   from zipfile import ZipFile   sentence_url='http://www.manythings.org/anki/deu-eng.zip'   r=requests.get(sentence_url)   z=ZipFile(io.BytesIO(r.content))   file=z.read('deu.txt')   #Format data   eng_ger_data=file.decode()   eng_ger_data=eng_ger_data.encode('ascii', errors='ignore')   eng_ger_data=eng_ger_data.decode().split('\n')   eng_ger_data=[[x.split('\t') for x in eng_ger_data if len(x)>=1]   [english_sentence, german_sentence]=[list(x) for x in zip(*eng_ger_data)]   print(len(english_sentence))   # 137673   print(len(german_sentence))   # 137673   print(eng_ger_data[10])

8）其他资源：

TensorFlow官方Python API文档网址：https://www.tensorflow.org/api_docs/python
TensorFlow官方教程网址：https://www.tensorflow.org/tutotials/index.html
TensorFlow官方GitHub仓库网址：https://github.com/tensorflow/tensorflow
TensorFlow在Dockerhub维护的Docker镜像：https://hub.docker.com/tensorflow/tensorflow
Stack Overflow上有关TensorFlow的知识问答http://stackoverflow.com/questions/tagged /TensorFlow
Google在在线课程Udacity上开课网址https://www.udacity.com/course/deep-learning--ud730
TensorFlow提供的网站，可以可视化查看随着参数和样本数据集变化对训练神经网络的影响，网址：http://playground.tensorflow.org
深度学习开拓者Geoffrey Hinton在Coursera上开课教授“机器学习中的神经网络”，网址：https://www.coursera.org/learn/neural-networks
斯坦福大学提供在线课程“图像识别中卷积神经网络”及课件，网址：http://cs231n.stanford.edu/
教材在GitHub的代码：https://github.com/nfmcclure/tensorflow_cookbook
Packt代码库：https://github.com/PacktPublishing/TensorFlow-Machine-Learning-Cookbook -Second-Edition

2. 使用TensorFlow创建简单分类器：

1）传入一个列表到计算图中操作：

import tensorflow as tf sess=tf.Session() import numpy as np x_vals=np.array([1., 3., 5., 7., 9.]) x_data=tf.placeholder(tf.float32) m_const=tf.constant(3.) my_product=tf.multiply(x_data, m_const) for x_val in x_vals: print(sess.run(my_product, feed_dict={x_data: x_val}))
上述代码中声明了张量和占位符，创建一个numpy数组传入计算图操作，打印返回值。

2）嵌入Layer：

import tensorflow as tf import numpy as np sess=tf.Session() # 创建数据和占位符 my_array=np.array([[1., 3., 5., 7., 9.], [-2., 0., 2., 4., 6.], [-6., -3., 0., 3., 6.]]) x_vals=np.array([my_array, my_array+1]) x_data=tf.placeholder(tf.float32, shape=(3, 5)) # 创建常量矩阵 m1=tf.constant([[1.], [0.],[-1.], [2.], [4.]]) m2=tf.constant([[2.]]) a1=tf.constant([[10.]]) # 声明操作，表示为计算图 prod1=tf.matmul(x_data, m1) prod2=tf.matmul(prod1, m2) add1=tf.add(prod2, a1) # 传入数据，打印结果 for x_val in x_vals: print(sess.run(add1, feed_dict={x_data: x_val}))
上述代码中，传入两个3×5的numpy数组，然后乘以5×1的常量矩阵，将返回一个3×1的矩阵；接着再乘以1×1的常量矩阵，返回结果仍为3×1的矩阵；最后加上一个3×1的矩阵。
用计算图运行之前，需要先预估声明数据的形状以及操作返回值的形状。为了实现目标，要指明变化的维度，如事先不知道维度设为None。示例：
x_data=tf.placeholder(tf.float32, shape=(3, None))
上面是在占位符列数未知时使用的方式，但乘以的常量矩阵要有一致的行数。None维度主要应用在限制训练或者测试时的数据批量大小方面，也即一次计算时有多少个数据点参与运算。

3）嵌入多层Layer：

  import tensorflow as tf   import numpy as np   sess=tf.Session()   # 通过numpy创建2D图像，4×4像素，四维--图片数量、高度、宽度、颜色通道   x_shape=[1, 4, 4, 1]   x_val=np.random.uniform(size=x_shape)   # 创建占位符，用来传入图片   x_data=tf.placeholder(tf.float32, shape=(3, 5))   # 使用TensorFlow内建函数conv2d()   my_filter=tf.constant(0.25, shape=[2, 2, 1, 1])   my_strides=[1, 2, 2, 1]   mov_avg_layer=tf.nn.conv2d(x_data, my_filter, my_strides, padding='SAME', name='Moving_Avg_Window')
TensorFlow内建函数conv2d()可以传入滑度窗口、过滤器、步长，在滑度窗口的4个方向上计算，因此4个方向都要指定步长。这里创建一个2×2的窗口，为了计算平均值，用常量0.25与2×2的窗口卷积，使用函数的name参数将此层命名。可以使用公式Output = ( W - F + 2P ) / S + 1计算卷积层的返回值形状，其中W为输入形状，F为过滤器形状，P为Padding的大小，S为步长形状。
下面需要定义Layer来操作滑动窗口平均的2×2的返回值。自定义函数将输入张量乘以一个2×2的矩阵张量，然后每个元素加1。因为矩阵运算只计算二维矩阵，所以剪裁图像的多余维度，通过TensorFlow的内建函数squeeze()实现剪裁。代码：
  def custom_layer(input_matrix):      input_matrix_squeezed=tf.squeeze(input_matrix)      A=tf.constant([[1., 2.], [-1., 3.]])      b=tf.constant(1., shape=[2,2])      temp1=tf.matmul(A, input_matrix_squeezed)      temp=tf.add(temp1, b) # Ax+b      return tf.sigmoid(temp)
把自定义的Layer加入到计算图，并且用tf.name_scope()命名唯一的Layer名字，以便在计算图中显示时可以折叠/扩展custom_layer层。代码：
  with tf.name_scope('Custom_Layer') as scope:      custom_layer1=custom_layer(mov_avg_layer)   # 为占位符传入4×4像素图片，然后执行计算图   print(sess.run(custom_layer1, feed_dict={x_data: x_val}))

4）实现损失函数：

损失函数(loss function)对机器学习非常重要，它们用来度量模型输出值与目标值间的差值。
⑴ 回归损失函数：
  import matplotlib.pyplot as plt   import tensorflow as tf   # 创建预测序列和目标序列张量，预测序列是-1到1之间的等差数列   x_vals=tf.linspace[-1., 1., 500]   target=tf.constant(0.)   # L2正则损失函数，即预测值与目标值之间的差值的平方和   l2_y_vals=tf.square(target-x_vals)   l2_y_out=sess.run(l2_y_vals)   # L1正则损失函数，对差值求绝对值   l1_y_vals=tf.abs(target-x_vals)   l1_y_out=sess.run(l1_y_vals)   # Pseudo-Huber损失函数，表达式依赖delta   delta1=tf.constant(0.25)   phuber1_y_vals=tf.multiply(tf.square(delta1),        tf.sqrt(1.+tf.square((target-x_vals)/delta1))-1.)   phuber1_y_out=sess.run(phuber1_y_vals)   delta2=tf.constant(5.)   phuber2_y_vals=tf.multiply(tf.square(delta2),        tf.sqrt(1.+tf.square((target-x_vals)/delta2))-1.)   phuber2_y_out=sess.run(phuber2_y_vals)
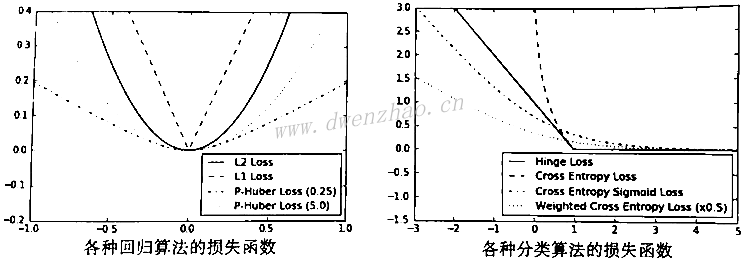
上面使用的是回归算法的损失函数，回归算法是预测连续因变量的。其中，L2正则损失函数也称欧拉损失函数，计算的是预测值与目标值差值的平方和，其在目标值附近有很好的曲度，机器学习利用此点收敛，并且离目标越近收敛越慢。TensorFlow有内建的L2正则形式nn.l2_loss()，但这个函数其实是L2正则的一半。L1正则损失函数也称绝对值损失函数，其对差值求绝对值，优势在于当误差较大时不会变得更陡峭，但在目标值附近不平滑，会导致不能很好地收敛。
Pseudo-Huber损失函数是Huber损失函数的连续、平滑估计，试图利用L1和L2正则消减极值附近的陡峭，使得目标值附近连续，其表达式依赖于参数delta。
⑵ 分类损失函数：
分类损失函数是用来评估预测分类结果的。通常，模型对分类的输出为一个0~1之间的实数，然后选定一个截止点，并根据输出是否高于此点进行分类。
  x_vals=tf.linspace[-3., 5., 500]   target=tf.constant(1.)   targets=tf.fill([500,], 1.)   # Hinge损失函数，这里计算两个目标类之间的损失   hinge_y_vals=tf.maximum(0., 1.-tf.multify(target, x_vals))   hinge_y_out=sess.run(hinge_y_vals)   # 两类交叉熵损失函数Cross-entropy loss   xentropy_y_vals=-tf.multiply(target, tf.log(x_vals))-tf.multiply((1.-target), tf.log(1.-x_vals))   xentropy_y_out=sess.run(xentropy_y_vals)   # Sigmoid交叉熵损失，先把x_vals通过sigmoid函数转换再计算交叉熵   xentropy_sigmoid_y_vals=tf.nn.sigmoid_cross_entropy_with_logits_v2(logits=x_vals, labels=targets)   xentropy_sigmoid_y_out=sess.run(xentropy_sigmoid_y_vals)   # 加权交叉熵损失   weight=tf.constant(0.5)   xentropy_weighted_y_vals=tf.nn.weighted_cross_entropy_with_logits(logits=x_vals, labels=targets, pos_weight=weight)   xentropy_weighted_y_out=sess.run(xentropy_weighted_y_vals)   # Softmax交叉熵损失函数   unscaled_logits=tf.constant([[1., -3., 10.]])   target_dist=tf.constant([[0.1, 0.02, 0.88]])   softmax_xentropy=tf.nn.softmax_cross_entropy_with_logits_v2(logits=unscaled_logits, labels=target_dist)   print(sess.run(softmax_xentropy))   # [1.16012561]   # 稀疏Softmax交叉熵损失函数   unscaled_logits=tf.constant([[1., -3., 10.]])   sparse_target_dist=tf.constant([2])   sparse_xentropy=tf.nn.sparse_softmax_cross_entropy_with_logits(logits=unscaled_logits, labels=sparse_target_dist)   print(sess.run(sparse_xentropy))   # [0.00012564]
Hinge损失函数主要用于评估支持向量机算法，也有时用来评估神经网络算法；两类交叉熵损失函数Cross-entropy loss有时作为逻辑损失函数，当预测两类目标0或1时，希望度量预测值到真实分类值(0/1)的距离，为0到1之间的实数，就可以用信息论中的交叉熵；Sigmoid交叉熵损失函数Sigmoid cross entropy loss是先把值通过sigmoid函数转换，然后再计算交叉熵；加权交叉熵损失函数Weighted cross entropy loss是Sigmoid交叉熵损失函数的加权，对正目标加权；Softmax交叉熵损失函数Softmax cross entropy loss是作用于非归一化的输出结果，通过Softmax函数将输出结果转化成概率分布，然后计算真值概率分布的损失，只对单一目标的分类计算损失；稀疏Softmax交叉熵损失函数Sparse softmax cross entropy loss是把目标分类为true的转化成index。
⑶ 绘制损失函数曲线：
用matplotlib绘制回归算法的损失函数：
  x_array=sess.run(x_vals)   plt.plot(x_array, l2_y_out, 'b-', label='L2 Loss')   plt.plot(x_array, l1_y_out, 'r--', label='L1 Loss')   plt.plot(x_array, phuber_y_out, 'k-.', label='P-Huber Loss(0.25)')   plt.plot(x_array, phuber_y_out, 'k-:', label='P-Huber Loss(5.0)')   plt.ylim(-0.2, 0.4')   plt.legend(loc='lower right', prop={'size':11})   plt.show()
用matplotlib绘制分类算法的损失函数：
  x_array=sess.run(x_vals)   plt.plot(x_array, hinge_y_out, 'b-', label='Hinge Loss')   plt.plot(x_array, xentropy_y_out, 'r--', label='Cross Entropy Loss')   plt.plot(x_array, xentropy_sigmoid_y_out, 'k-.', label='Cross Entropy Sigmoid Loss')   plt.plot(x_array, xentropy_weighted_y_out, 'g:', label='Weighed Cross Entropy Loss(x0.5)')   plt.ylim(-1.5, 3')   plt.legend(loc='lower right', prop={'size':11})   plt.show()
绘制出来的损失函数图形为：
TensorFlow的损失函数图形
⑷ 损失函数比较：

损失函数	使用类型	优点	缺点
L2	回归算法	更稳定	缺少健壮
L1	回归算法	更健壮	缺少稳定
Pseudo-Huber	回归算法	更健壮、稳定	参数多
Hinge	分类算法	常用于SVM的最大距离	异常值导致无边界损失
Cross-entropy	分类算法	更稳定	缺少健壮。出现无边界损失

分类算法一般使用交叉熵损失函数，Sigmoid交叉熵损失函数被用在非归一化逻辑操作，先计算sigmoid再计算交叉熵。TensorFlow有很好的内建方法来处理边界问题。
大部分分类算法损失函数是针对着二分类预测，不过也可以通过对每个预测值/目标的交叉熵求和，扩展成多分类。
⑸ 评价机器学习模型的指标：

模型指标	描述
R平方值R-squared	对简单的线性模型来说，用于度量因变量的变异中可由自变量解释部分所占的比例
RMSE(均方根误差)	对连续模型来说，平均方差是度量预测的值和观察到的值之差的样本标准差
混淆矩阵(Confusion matrix)	对分类模型而说，以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的分类判断两个标准进行分析汇总，其每一列代码预测值，每一行代表的是实际的类别。理想情况下，混淆矩阵是对角矩阵
召回率(Recall)	对于分类模型来说，召回率是正类预测为正类数与所有预测正类数的比值
精准度(Precision)	对于分类模型来说，精准度是正类预测为正类数与所有实际正类数的比值
F值(F-score)	对于分类模型来说，F值是召回率和精准度的调和平均数

5）反向传播：

使用TensorFlow的一个优势是，可以维护操作状态和基于反向传播自动地更新模型变量。
TensorFlow能通过计算图来实现最小化损失函数的误差反向传播，进而更新变量，这是依靠优化函数来实现的。一旦声明好优化函数，TensorFlow将通过优化函数在所有计算图中解决反向传播的项，当传入数据，最小化损失函数，TensorFlow会在计算图中根据状态相应地调节变量。
⑴ 回归算法示例：
从均值为1、标准差为0.1的正态分布中抽取随机数，然后乘以变量A，目标值10，损失函数为L2正则损失函数。
  import tensorflow as tf   import numpy as np   sess=tf.Session()   x_vals=np.random.normal(1, 0.1, 100)   y_vals=np.repeat(10., 100)   x_data=tf.placeholder(shape=[1], dtype=tf.float32)   y_target=tf.placeholder(shape=[1], dtype=tf.float32)   A=tf.Variable(tf.random_normal(shape=[1]))   my_output=tf.mul(x_data, A)   # L2正则损失函数   loss=tf.square(my_output-y_target)
然后需要声明变量的优化器。大部分优化器算法需要知道每步迭代的步长，这是由学习率控制的。如果学习率太小，机器学习算法可能耗时很长才能收敛；如果学习率太大，机器学习算法可能会跳过最优点。不同的问题要使用不同的优化器算法，这里使用标准梯度下降算法。
  my_opt=tf.train.GradientDescentOptimizer(learning_rate=0.02)   train_step=my_opt.minimize(loss)   # 运行之前初始化变量   init=tf.global_variable_initializer()   sess.run(init)
最后是训练算法，其中迭代101次，并且每25次迭代打印结果。选择一个随机的x和y传入计算图，TensorFlow将自动计算损失，调整A偏差来最小化损失。代码：
  for i in range(100):      rand_index=np.random,choice(100)      rand_x=[x_vals[rand_index]]      rand_y=[y_vals[rand_index]]      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      if (i+1) % 25 ==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A)))        print('Loss='+str(sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})))
部分输出结果：
  Step #75 A=[9.37753201]   Loss=3.03149   Step #100 A=[9.80041122]   Loss=0.0990248
理论上A的最优解为10。
⑵ 分类算法示例：
简单的二值分类算法，从两个正态分布N(-1,1)和N(3,1)生成100个数，所有从N(-1,1)生成的目标数据标为目标类0，从正态分布N(3,1)生成的数据标为目标类1，模型算法通过sigmoid函数将这些生成的数据转换成目标数据，即模型算法为sigmoid(x+A)，其中A是要拟合的变量，理论上A=-1。假设两个正态分布的均值分别是m1和m2，则达到A的取值时，它们通过-(m1+m2)/2转换成到0等距的值。同时，指定一个合适的学习率对机器学习算法的收敛有利，优化器类型使用标准梯度下降法GradientDescentOptimizer()。
  # 重置前面的计算图，然后可以使用相同的脚本进行分类算法   from tensorflow.python.framework import as ops   ops.reset_default_graph()   sess=tf.Session()   # 从正态分布(N(-1,1), N(3,1))生成数据，也生成目标标签、占位符和偏差变量A   x_vals=np.concatenate((np.random.normal(-1,1,50),np.random.normal(3,1,50)))   y_vals=np.concatenate((np.repeat(0.,50),np.repeat(0.,50)))   x_data=tf.placeholder(shape=[1],dtype=tf.float32)   y_target=tf.placeholder(shape=[1],dtype=tf.float32)   A=tf.Variable(tf.random_normal(mean=10,shape[1]))   # 增加转换操作   my_output=tf.add(x_data,A)   # 为批量数据增加一个维度以符合损失函数要求   my_output_expanded=tf.expand_dims(my_output,0)   y_target_expanded=tf.expand_dims(y_target,0)   # 初始化变量A   init=tf.global_variable_initializer()   sess.run(init)   # 声明损失函数，使用带非归一化logits的交叉熵的损失函数   xentropy=tf.nn.sigmoid_cross_entropy_with_logits(my_output_expanded, y_target_expanded)   # 增加一个优化器以更新变量   my_opt=tf.train.GradientDescrentOptimizer(0.05)   train_step=my_opt.minimize(xentropy)
最后，通过随机选择的数据迭代几百次，相应更新变量A，每迭代200次打印出损失和变量A的返回值：
  for i in range(1400):      rand_index=np.random.choice(100)      rand_x=[x_vals[rand_index]]      rand_y=[y_vals[rand_index]]      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      if (i+1) % 200 ==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A)))        print('Loss='+str(sess.run(xentropy, feed_dict={x_data: rand_x, y_target: rand_y})))
部分输出结果：
  Step #1000 A=[-0.90859312]   Loss=[[0.02346182]]   Step #1400 A=[-1.08486211]   Loss=[[0.04099189]]
理论上A的最优解为-1。
⑶ 操作过程总结：
  ·  生成数据：所有样本都需要通过占位符进行加载
  ·  初始化占位符和变量：分类算法加了一个偏差变量
  ·  创建损失函数：回归问题和分类问题使用了不同的损失函数
  ·  定义优化器算法：这里都使用了梯度下降算法
  ·  通过随机随机样本进行迭代，更新变量
优化器算法对学习率的选择比较敏感。小学习率收敛慢但结果精确，大学习率收敛快但结果不精确。如果算法不稳定要先降学习率，若算法收敛太慢可提高学习率。
有时，标准梯度下降算法会明显卡顿或收敛变慢，特别是在梯度为0的附近点，为此TensorFlow的MomentumOptimizer()函数增加了一项势能，是前一次迭代过程的梯度下降值的倒数。
还可以改变步长，理想情况下，对于变化小的变量使用大步长，而对变化迅速的变量使用小步长。实现这种优点的常用算法是Adagrad，此算法考虑整个历史迭代的变量梯度，TensorFlow中使用AdagradOptimizer()实现。但由于Adagrad算法计算整个历史迭代的梯度会导致梯度迅速变为0，解决这个问题用Adadelta算法，它限制使用的迭代次数，TensorFlow中用AdadeltaOptimizer()实现。

6）批量训练和随机训练：

为了TensorFlow计算变量梯度来让反向传播工作，必须度量一个或多个样本的损失，随机训练会一次随机抽样训练数据和目标数据对来完成训练，也可以一次大批量训练取平均损失来进行梯度计算，批量训练大小可以一次上扩到整个数据集。
  # 声明批量大小，指通过计算图一次传入的训练数据数量   batch_size=20   # 声明模型的数据、占位符和变量   x_vals=np.random.normal(1, 0.1, 100)   y_vals=np.repeat(10., 100)   x_data=tf.placeholder(shape=[None, 1], dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1], dtype=tf.float32)   A=tf.Variable(tf.random_normal(shape=[1, 1]))
代码中改变了占位符的形状，占位符有两个维度，可以显式地设维度为20，也可以设为None。
计算图中要加入矩阵乘法，矩阵乘法不满足交换律，所以要注意顺序。
  my_output=tf.matmul(x_data, A)
然后定义损失函数，损失函数是每个数据点L2损失的平均值，通过TensorFlow提供的reduce _mean()函数实现。
  loss=tf.reduce_mean(tf.square(my_output-y_target))   # 声明优化器   my_opt=tf.train.GradientDescentOptimizer(0.02)   train_step=my_opt.minimize(loss)   # 初始化模型变量   init=tf.global_variable_initializer()   sess.run(init)   # 训练中通过循环迭代优化模型算法   loss_batch=[]   for i in range(100):      rand_index=np.random,choice(100, size=batch_size)      rand_x=np.transpose([x_vals[rand_index]])      rand_y=np.transpose([y_vals[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      if (i+1) % 5 ==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A)))        temp_loss=sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})))        print('Loss='+str(temp_loss))        loss_batch.append(temp_loss)
上述代码是为了绘制损失图并与随机训练进行对比，初始化一个列表每间隔5次迭代保存损失函数。迭代100次输出最终返回值为：
  Step #100 A=[[9.86720943]]   Loss=0.
批量训练和随机训练的不同之处在于优化器和收敛过程，随机训练损失不规则，而批量训练损失更平滑，但找到一个合适的批量大小比较困难。使用批量训练可以快速得到最小损失，但会耗费更多计算资源。

7）创建分类器：

加载鸢尾花的样本数据集，实现一个简单的二值分类器，用来预测一朵花是否为山鸢尾。
  import matplotlib.pyplot as plt   import numpy as np   from sklearn import datasets   import tensorflow as tf   sess=tf.Session()   # 导入鸢尾花数据集   iris=datasets.load_iris()   binary_target=np.array([1. if x==0 else 0. for x in iris.target])   iris_2d=np.array([x[2], x[3]] for x in iris.data])
代码中根据目标数据是否为山鸢尾将其转换成1或者0。由于原数据集将山鸢尾标记为0，将其转为1，同时把其他种类标记为0。训练只使用花瓣长度和宽度，在x-value特征值的第3列和第4列。
  # 声明批量训练大小、数据占位符和模型变量   batch_size=20   x1_data=tf.placeholder(shape=[None, 1], dtype=tf.float32)   x2_data=tf.placeholder(shape=[None, 1], dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1], dtype=tf.float32)   A=tf.Variable(tf.random_normal(shape=[1, 1]))   b=tf.Variable(tf.random_normal(shape=[1, 1]))
数据占位符的第一维度设为None，指定dtype=tf.float32降低float字节数，可以提高算法的性能。
下面是定义线性模型，表达式为x2=x1*A+b。如果找到的数据点在直线之上，将数据点代入x2 - x1*A-b，计算出的结果大于0；而找到的数据点在直线以下，将数据点代入x2 - x1*A-b，计算的结果小于0。将公式传入sigmoid函数，然后预测结果1或者0。
  my_mult=tf.matmul(x2_data, A)   my_add=tf.add(my_mult, b)   my_output=tf.sub(x1_data, my_add)
使用sigmoid交叉熵损失函数：
  xentropy=tf.nn.sigmoid_cross_entropy_with_logits(my_output, y_target)
声明优化器，使用最小化交叉熵损失，选择学习率0.05：
  my_opt=tf.train.GradientDescentOptimizer(0.02)   train_step=my_opt.minimize(xentropy)   # 初始化模型变量   init=tf.global_variable_initializer()   sess.run(init)
训练线性模型，迭代1000次，传入花瓣长度、花瓣宽度和目标变量三种数据，每200次迭代打印变量值：
  for i in range(1000):      rand_index=np.random,choice(len(iris_2d), size=batch_size)      rand_x=iris_2d[rand_index]      rand_x1=np.array([[x[0]] for x in rand_x])      rand_x2=np.array([[x[1]] for x in rand_x])      rand_y=np.array([[y] for y in binary_target[rand_index]])      sess.run(train_step, feed_dict={x1_data: rand_x1, x2_data: rand_x2, y_target: rand_y})      if (i+1) % 200 ==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A))+', b='+str(sess.run(b)))
下面抽取模型变量并绘图：
  [[slope]]=sess.run(A)   [[intercept]]=sess.run(b)   x=np.linspace(0, 3, num=50)   ablineValues=[]   for i in x:      ablineValues.append(slope*i+intercept)   setosa_x=[a[1] for i,a in enumerate(iris_2d) if binary_target[i]==1]   setosa_y=[a[0] for i,a in enumerate(iris_2d) if binary_target[i]==1]   non_setosa_x=[a[1] for i,a in enumerate(iris_2d) if binary_target[i]==0]   non_setosa_y=[a[0] for i,a in enumerate(iris_2d) if binary_target[i]==0]   plt.plot(setosa_x, setosa_y, 'rx', ms=10, mew=2, label='setosa')   plt.plot(non_setosa_x, non_setosa_y, 'ro', label='Non_setosa')   plt.plot(x, ablineValues, 'b-')   plt.xlim([0.0, 2.7])   plt.ylim([0.0, 7.1])   plt.subtitle('Linear' Separator For I.setosa', fontsize=20)   plt.xlabel('Petal Length')   plt.ylabel('Petal Width')   plt.Legend(loc='lower right')   plt.show()
目的是利用花瓣长度和花瓣宽度特征在山鸢尾与其他品种之间拟合一条直线，绘制所有数据点和拟合结果。这种用直线分割两类目标并不是最好的模型。

8）模型评估：

模型评估非常重要，每个模型都有多种评估方式，使用TensorFlow时需要把模型评估加入到计算图中，然后在模型训练完成后调用模型评估。在模型训练过程中，模型评估可以洞察模型算法，给出提示信息调试，提高或者改变整个模型。
模型评估需要使用大量数据点，如果使用批量训练，可以重用模型来预测批量数据点，但如果使用随机训练，就不得不创建单独的评估器来处理批量数据点。
回归算法用来预测连续数值型，其目标是数值。为了评估回归预测值是否与实际目标相符，需要度量两者之间的距离。
分类算法模型基于数值型输入预测分类值，实际目标是1和0的序列。分类算法模型的损失函数一般不容易解释模型好坏，要看准确预测分类的结果的百分比。
⑴ 评估回归算法模型：
  import matplotlib.pyplot as plt   import numpy as np   from sklearn import datasets   import tensorflow as tf   sess=tf.Session()   x_vals=np.random.normal(1, 0.1, 100)   y_vals=np.repeat(10., 100)   x_data=tf.placeholder(shape=[None, 1], dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1], dtype=tf.float32)   batch_size=25
将数据集随机分割成训练数据集和测试数据集：
  train_indices=np.random.choice(len(x_vals)), round(len(x_vals)*0.8), replace=False)   test_indices=np.array(list(set(range(len(x_vals)))-set(train_indices)))   x_vals_train=x_vals[train_indices]   x_vals_test=x_vals[test_indices]   y_vals_train=y_vals[train_indices]   y_vals_test=y_vals[test_indices]   A=tf.Variable(tf.random_normal(shape=[1, 1]))
声明算法模型、损失函数和优化器算法，初始化模型变量A：
  my_output=tf.matmul(x_data, A)   loss=tf.reduce_mean(tf.square(my_output-y_target))   my_opt=tf.train.GradientDescentOptimizer(0.02)   train_step=my_opt.minimize(loss)   init=tf.global_variable_initializer()   sess.run(init)
迭代训练模型：
  for i in range(100):      rand_index=np.random,choice(len(x_vals_train), size=batch_size)      rand_x=np.transpose([x_vals_train[rand_index]])      rand_y=np.transpose([y_vals_train[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      if (i+1) % 25 ==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A)))        print('Loss='+str(sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})))
为了评估训练模型，打印训练数据集和测试数据集训练的MSE损失函数值：
  mse_test=sess.run(loss, feed_dict={x_data: np.transpose([x_vals_test]),        y_target: np.transpose([y_vals_test])})   mse_train=sess.run(loss, feed_dict={x_data: np.transpose([x_vals_train]),        y_target: np.transpose([y_vals_train])})   print('MSE on test: '+str(np.round(mse_test, 2)) # MSE on test: 1.35   print('MSE on train: '+str(np.round(mse_train, 2)) # MSE on test: 0.88
⑵ 评估分类算法模型：
  from tensorflow.python.framework import as ops   ops.reset_default_graph()   sess=tf.Session()   batch_size=25   x_vals=np.concatenate((np.random.normal(-1,1,50),np.random.normal(2,1,50)))   y_vals=np.concatenate((np.repeat(0.,50),np.repeat(1.,50)))   x_data=tf.placeholder(shape=[1, None],dtype=tf.float32)   y_target=tf.placeholder(shape=[1, None],dtype=tf.float32)   train_indices=np.random.choice(len(x_vals)), round(len(x_vals)*0.8), replace=False)   test_indices=np.array(list(set(range(len(x_vals)))-set(train_indices)))   x_vals_train=x_vals[train_indices]   x_vals_test=x_vals[test_indices]   y_vals_train=y_vals[train_indices]   y_vals_test=y_vals[test_indices]   A=tf.Variable(tf.random_normal(mean=10,shape[1]))
声明算法模型、损失函数和优化器算法，初始化模型变量A：
  my_output=tf.add(x_data, A)   init=tf.global_variable_initializer()   sess.run(init)   xentropy=tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(my_output, y_target))   my_opt=tf.train.GradientDescrentOptimizer(0.05)   train_step=my_opt.minimize(xentropy)
训练迭代：
  for i in range(1800):      rand_index=np.random.choice(len(x_vals_train), size=batch_size)      rand_x=[x_vals_train[rand_index]]      rand_y=[y_vals_train[rand_index]]      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      if (i+1) % 200 ==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A)))        print('Loss='+str(sess.run(xentropy, feed_dict={x_data: rand_x, y_target: rand_y})))
为了评估模型，创建预测操作，并用squeeze()函数封装预测操作，使得预测值与目标值具有相同的维度，然后用equal()函数检测是否相等，把得到的true和false的boolean型张量转化成float32型，再对其取平均值，得到一个准确度值。代码：
  y_prediction=tf.squeeze(tf.round(tf.nn.sigmoid(tf.add(x_data, A))))   correct_prediction=tf.equal(y_prediction, y_target)   accuracy=tf.reduce_mean(tf.cast(correct_prediction, tf.float32))   acc_value_test=sess.run(accuracy, feed_dict={x_data: [x_vals_test], y_data: [y_vals_test]})   acc_value_train=sess.run(accuracy, feed_dict={x_data: [x_vals_train], y_data: [y_vals_train]})   print('Accuracy on train set: '+str(acc_value_train))   # Accuracy on train set: 0.925   print('Accuracy on test set: '+str(acc_value_test))   # Accuracy on test set: 0.95
模型训练结果，如准确度、MSE等，有助于评估机器学习模型。对于一维模型，很容易绘制模型和数据点，用matplotlib绘制两个分开的直方图来可视化机器学习模型和数据点：
  A_result=sess.run(A)   bins=np.linspace(-5, 5, 50)   plt.hist(x_vals[0:50], bins, alpha=0.5, label='N(-1,1)', color='write')   plt.hist(x_vals[50:100], bins[0:50], alpha=0.5, label='N(2,1)', color='red')   plt.plot((A_result, A_result), (0, 8), 'k--', linewidth=3, label='A='+str(np.round(A_result, 2)))   plt.legend(loc="upper right")   plt.title('Binary Classifier, Accuracy='+str(np.round(acc_value, 2)))   plt.show()

3. 基于TensorFlow的线性回归：

线性回归算法是统计分析、机器学习和科学计算中最重要、最常使用的算法之一。

1）通过求逆矩阵方法解决二维线性回归问题：

线性回归算法能表示为矩阵计算Ax=b，要解决的是用矩阵x来求解系数。如果观测矩阵不是方阵，求解出的矩阵x为x=(A^TA)^-1A^Tb。下面将生成二维数据，用TensorFlow来求解，然后绘制结果。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   sess=tf.Session()   x_vals=np.linspace(0, 10, 100)   y_vals=x_vals+np.random.normal(0, 1, 100)
创建A矩阵，为矩阵x_vals_column和ones_column的合并；然后以矩阵y_vals创建b矩阵：
  x_vals_column=np.transpose(np.matrix(x_vals))   ones_column=np.transpose(np.matrix(np.repeat(1, 100)))   A=np.column_stack((x_vals_column, ones_column))   b=np.transpose(np.matrix(y_vals))
将A和b矩阵转换成张量：
  A_tensor=tf.constant(A)   b_tensor=tf.constant(b)
使用TensorFlow的tf.matrix_inverse()方法：
  tA_A=tf.matmul(tf.transpose(A_tensor), A_tensor)   tA_A_inv=tf.matrix_inverse(tA_A)   product=tf.matmul(tA_A_inv, tf.transpose(A_tensor))   solution=tf.matmul(product, b_tensor)   solution_eval=sess.run(solution)
从解中抽取系数、斜率和y截距y_intercept：
  slope=solution_eval[0][0]   y_intercept=solution_eval[1][0]   print('slope: '+str(slope))   print('y_intercept: '+str(y_intercept))   best_fit=[]   for i in x_vals:      best_fit.append(slope*i+y_intercept)   plt.plot(x_vals, y_vals, 'o', label='Data')   plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)   plt.legend(loc='upper left')   plt.show()
上述代码是通过矩阵操作直接求解结果，仅仅为了说明TensorFlow的灵活用法。多数情况下通过求逆矩阵方法是低效的，特别是当矩阵非常大时效率更低。大部分TensorFlow算法是通过迭代训练实现的，利用反向传播自动更新模型变量。

2）实现矩阵分解：

直接求逆矩阵常常低效，使用矩阵分解的方法能提高效率。Cholesky矩阵分解法把一个矩阵分解为下三角矩阵L和上三角矩阵L'，而L和L'互为转置矩阵。这样，求解Ax=b可以改写为LL'x=b，首先求解Ly=b，然后求解L'x=y，就得到系数矩阵x。TensorFlow有内建的Cholesky矩阵分解函数。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   from tensorflow.python.framework import ops   ops.reset_default_graph()   sess=tf.Session()   x_vals=np.linspace(0, 10, 100)   y_vals=x_vals+np.random.normal(0, 1, 100)   x_vals_column=np.transpose(np.matrix(x_vals))   ones_column=np.transpose(np.matrix(np.repeat(1, 100)))   A=np.column_stack((x_vals_column, ones_column))   b=np.transpose(np.matrix(y_vals))   A_tensor=tf.constant(A)   b_tensor=tf.constant(b)
找到方阵的Cholesky矩阵分解A^TA：
  tA_A=tf.matmul(tf.transpose(A_tensor), A_tensor)   L=tf.cholesky(tA_A)   tA_b=tf.matmul(tf.transpose(A_tensor), b)   sol1=tf.matrix_solve(L, tA_b)   sol2=tf.matrix_solve(tf.transpose(L), sol1)
TensorFlow的cholesky()函数仅仅返回矩阵分解的下三角矩阵，因为上三角矩阵是下三角矩阵的转置矩阵。然后抽取系数：
  solution_eval=sess.run(sol2)   slope=solution_eval[0][0]   y_intercept=solution_eval[1][0]   print('slope: '+str(slope))   print('y_intercept: '+str(y_intercept))   best_fit=[]   for i in x_vals:      best_fit.append(slope*i+y_intercept)   plt.plot(x_vals, y_vals, 'o', label='Data')   plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)   plt.legend(loc='upper left')   plt.show()
通过分解矩阵方法求解有时更高效，并且数值稳定。

3）实现线性回归：

TensorFlow求解斜率和截距可以通过迭代方法。通过遍历批量数据点并让TensorFlow更新斜率和截距，数据使用Scikit Learn的内建iris数据集，x值代表花瓣宽度，y值代表花瓣长度，找到最优直线，使用L2正则损失函数。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   from sklearn import datasets   from tensorflow.python.framework import ops   ops.reset_default_graph()   sess=tf.Session()   iris=datasets.load_iris()   x_vals=np.array([x[3] for x in iris.data])   y_vals=np.array([y[0] for y in iris.data])
声明学习率、批量大小、占位符和模型变量：
  learning_rate=0.05   batch_size=25   x_data=tf.placeholder(shape=[None, 1],dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1],dtype=tf.float32)   A=tf.Variable(tf.random_normal(shape[1, 1]))   b=tf.Variable(tf.random_normal(shape[1, 1]))
加入线性模型y=Ax+b：
  model_output=tf.add(tf.matmul(x_data, A), b)
声明L2损失函数，为批量损失的平均值，然后初始化变量，声明优化器：
  loss=tf.reduce_mean(tf.square(y_target-model_output))   init=tf.global_variables_initializer()   sess.run(init)   my_opt=tf.train.GradientDescentOptimizer(learning_rate)   train_step=my_opt.minimize(loss)
遍历迭代，并在随机选择的批量数据上进行模型训练。迭代100次，每25次迭代输出变量值和损失值，保存的损失值将用于后续的可视化。
  loss_vec=[]   for i in range(100):      rand_index=np.random.choice(len(x_vals), size=batch_size)      rand_x=np.transponse([x_vals[rand_index]])      rand_y=np.transponse([y_vals[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      temp_loss=sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})      loss_vec.append(temp_loss)      if (i+1) % 25==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A))+' b='+str(sess.run(b)))        print('Loss='+str(temp_loss))
抽取系数，创建最佳拟合曲线：
  [slope]=sess.run(A)   [y_intercept]=sess.run(b)   best_fit=[]   for i in x_vals:      best_fit.append(slope*i+y_intercept)
然后绘出拟合直线和迭代100次的L2正则损失函数曲线：
  plt.plot(x_vals, y_vals, 'o', label='Data Points')   plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)   plt.legend(loc='upper left')   plt.title('Sepal Length vs Petal Width')   plt.xlabel('Petal Width')   plt.ylabel('Sepal Length')   plt.show()   plt.plot(loss_vec, 'k-')   plt.title('L2 Loss per Generation')   plt.xlabel('Generation')   plt.ylabel('L2 Loss')   plt.show()
通过Loss曲线很容易看出算法模型是过拟合还是欠拟合。将数据集分割成测试数据集和训练数据集，如果训练数据集的准确性更大，而测试数据集准确度更低，那么是过拟合；如果在测试数据集和训练数据集上的准确度一直在增加，那么为欠拟合，需要继续训练。
如果上述代码中使用L1损失函数，并设置不同的学习率，可以对比曲线，看出两种损失函数的差别：当学习率为0.05时，L2正则损失函数更优，可获得更低的损失值；但当学习率增加到0.4时，会导致L2损失过大，而L1正则损失收敛。

4）实现戴明回归算法：

戴明回归(Deming Regression)也称全回归、正交回归ODR、最短路径回归，最小化到回归直线的总距离，其最小化x值和y值两个方向的误差。实现戴明回归需要修改损失函数。给定直线的斜率和截距，求解一个点到直线的垂直距离，代入几何公式并使距离最小化。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   from sklearn import datasets   sess=tf.Session()   iris=datasets.load_iris()   x_vals=np.array([x[3] for x in iris.data])   y_vals=np.array([y[0] for y in iris.data])   batch_size=50   x_data=tf.placeholder(shape=[None, 1],dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1],dtype=tf.float32)   A=tf.Variable(tf.random_normal(shape[1, 1]))   b=tf.Variable(tf.random_normal(shape[1, 1]))   model_output=tf.add(tf.matmul(x_data, A), b)
上面代码与前面的示例基本一样，然后声明损失函数。损失函数是由分子和分母组成的几何公式。给定直线的y=mx+b，点(x0, y0)到直线的距离表示为：
戴明回归算法公式
  deming_numerator=tf.abs(tf.sub(y_target, tf.add(tf.matmul(x_data, a),b)))   deming_demominator=tf.sqrt(tf.add(tf.square(A), 1)   loss=tf.reduce_mean(tf.truediv(deming_numerator, deming_demominator))
然后初始化变量，声明优化器，遍历迭代训练集以得到参数：
  init=tf.global_variables_initializer()   sess.run(init)   my_opt=tf.train.GradientDescentOptimizer(0.1)   train_step=my_opt.minimize(loss)   loss_vec=[]   for i in range(250):      rand_index=np.random.choice(len(x_vals), size=batch_size)      rand_x=np.transponse([x_vals[rand_index]])      rand_y=np.transponse([y_vals[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      temp_loss=sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})      loss_vec.append(temp_loss)      if (i+1) % 50==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A))+' b='+str(sess.run(b)))        print('Loss='+str(temp_loss))
绘制输出结果：
  [slope]=sess.run(A)   [y_intercept]=sess.run(b)   best_fit=[]   for i in x_vals:      best_fit.append(slope*i+y_intercept)   plt.plot(x_vals, y_vals, 'o', label='Data Points')   plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)   plt.legend(loc='upper left')   plt.title('Sepal Length vs Petal Width')   plt.xlabel('Petal Width')   plt.ylabel('Sepal Length')   plt.show()
戴明回归与线性回归算法得到的结果基本一致，两者之间的关键不同点在于预测值与数据点间的损失函数度量方式，线性回归算法的损失函数是竖直距离损失，而戴明回归算法是垂直距离损失（到x轴和y轴的总距离损失）。这里使用的戴明回归算法是总体回归类型，假设x值和y值的误差是相似的，也可以使用不同的误差来扩展x轴和y轴的距离计算。

5）实现lasso回归和岭回归算法：

有些正则算法可以限制回归算法输出结果中系数的影响，最常用的是lasso回归和岭回归。这两种算法通过在公式中增加正则项来限制斜率，目的是限制特征对因变量的影响，这通过增加一个依赖斜率的A的损失函数来实现。
对于lasso回归算法，在损失函数上增加一项是斜率A的某个给定倍数，在TensorFlow中使用阶跃函数的连续估计，其会在截止点跳跃扩大；对于岭回归算法，增加一个L2范数，即斜率系数L2正则。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   from sklearn import datasets   from tensorflow.python.framework import ops   ops.reset_default_graph()   sess=tf.Session()   iris=datasets.load_iris()   x_vals=np.array([x[3] for x in iris.data])   y_vals=np.array([y[0] for y in iris.data])   batch_size=50   learning_rate=0.001   x_data=tf.placeholder(shape=[None, 1],dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1],dtype=tf.float32)   A=tf.Variable(tf.random_normal(shape[1, 1]))   b=tf.Variable(tf.random_normal(shape[1, 1]))   model_output=tf.add(tf.matmul(x_data, A), b)
上面的代码与前面的示例基本一致，也使用鸢尾花数据集。然后增加损失函数，为改良过的连续阶跃函数，截止点设为0.9，即限制斜率系数不超过0.9。代码为：
  lasso_param=tf.constant(0.9)   heavyside_step=tf.truediv(1., tf.add(1., tf.exp(tf.multiply(-100., tf.substract(A, lasso_param)))))   regularization_param=tf.mul(heavyside_step, 99.)   loss=tf.add(tf.reduce_mean(tf.square(y_target-model_output)), regularization_param)
初始化变量和声明优化器：
  init=tf.global_variables_initializer()   sess.run(init)   my_opt=tf.train.GradientDescentOptimizer(0.1)   train_step=my_opt.minimize(loss)
遍历迭代运行，需要一段时间才会收敛，最好显式斜率系数小于0.9。代码为：
  loss_vec=[]   for i in range(1500):      rand_index=np.random.choice(len(x_vals), size=batch_size)      rand_x=np.transponse([x_vals[rand_index]])      rand_y=np.transponse([y_vals[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      temp_loss=sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})      loss_vec.append(temp_loss)      if (i+1) % 300==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A))+' b='+str(sess.run(b)))        print('Loss='+str(temp_loss))
示例中通过在标准线性回归估计基础上增加一个连续的阶跃函数，实现lasso回归算法。由于阶跃函数的坡度，需要注意步长，步长太大会导致不收敛。
对于岭回归算法，只需要在上述代码上稍微改变损失函数即可：
  ridge_param=tf.contant(1.)   ridge_loss=tf.reduce_mean(tf.square(A))   loss=tf.expand_dims(tf.add(tf.reduce_mean(tf.square(y_target-model_output)),   tf.multiply(ridge_param, ridge_loss)), 0)

6）实现弹性网络回归算法：

弹性网络回归(Elastic Net Regression)是综合lasso回归和岭回归的一种回归算法，通过在损失函数中增加L1和L2正则项实现。
下面示例中，还是以iris数据集为训练数据，用花瓣长度、花瓣宽度和花萼宽度三个特征预测花萼长度。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   from sklearn import datasets   sess=tf.Session()
加载数据集，x_vals数据为三列值的数据：
  iris=datasets.load_iris()   x_vals=np.array([[x[1], x[2], x[3]] for x in iris.data])   y_vals=np.array([y[0] for y in iris.data])
然后声明批量大小、占位符、变量和模型输出，x_data占位符大小改变为3：
  batch_size=50   learning_rate=0.001   x_data=tf.placeholder(shape=[None, 3],dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1],dtype=tf.float32)   A=tf.Variable(tf.random_normal(shape[3, 1]))   b=tf.Variable(tf.random_normal(shape[1, 1]))   model_output=tf.add(tf.matmul(x_data, A), b)
对于弹性网络回归算法，损失函数包含斜率的L1正则和L2正则，创建L1正则和L2正则，并加入到损失函数中：
  elastic_param1=tf.constant(1.)   elastic_param2=tf.constant(1.)   l1_a_loss=tf.reduce_mean(tf.abs(A))   l2_a_loss=tf.reduce_mean(tf.square(A))   e1_term=tf.multiply(elastic_param1, l1_a_loss)   e2_term=tf.multiply(elastic_param2, l2_a_loss)   loss=expand_dims(tf.add(tf.reduce_mean(tf.square(y_target-model_output)), e1_term), e2_term), 0)
初始化变量，声明优化器，遍历迭代运行，训练拟合得到系数：
  init=tf.global_variables_initializer()   sess.run(init)   my_opt=tf.train.GradientDescentOptimizer(learning_rate)   train_step=my_opt.minimize(loss)   loss_vec=[]   for i in range(1000):      rand_index=np.random.choice(len(x_vals), size=batch_size)      rand_x=[x_vals[rand_index]]      rand_y=np.transponse([y_vals[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      temp_loss=sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})      loss_vec.append(temp_loss[0])      if (i+1) % 250==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A))+' b='+str(sess.run(b)))        print('Loss='+str(temp_loss))
绘制损失曲线：
  plt.plot(loss_vec, 'k-')   plt.title('Loss per Generation')   plt.xlabel('Generation')   plt.ylabel('Loss')   plt.show()
从曲线中可以看出随着训练迭代损失函数已经收敛。弹性网络回归算法的实现是多线性回归，增加L1和L2正则项后，损失函数的收敛变慢。

7）实现逻辑回归算法：

逻辑回归算法可以将线性回归转换成一个二值分类器，通过sigmoid函数将线性回归输出缩放到0和1之间。目标值是0或1代表着一个数据点是否属于某一类，如果预测值在截止值以上，预测值被标记为1类，否则预测值标记为0类。下面示例中指定截止值为0.5。
这里使用出生体重数据集，数据从GitHub下载：https://github.com/nfmcclure/tensorflow_cookbook/raw/master/01_Introduction/07_Working_with_Data_Sources/birthweight_data/birthweight.dat。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   import requests   from sklearn import datasets   from sklearn.preprocessing import normalize   from tensorflow.python.framework import ops   ops.reset_default_graph()   sess=tf.Session()
下面通过requests模块加载数据集，指定要使用的特征，而实际出生体重特征和Id两列不需要：
  birth_weight_file='birth_weight.csv'   if not os.path.exists(birth_weight_file):      birthdata_url='https://github.com/nfmcclure/tensorflow_cookbook/raw/master          /01_Introduction/7_Working_with_Data_Sources/birthweight_data/birthweight.dat'      birth_file=requests.get(birthdata_url)      birth_data=birth_file.text.split('\r\n')      birth_header=birth_data[0].split('\t')      birth_data=[[float(x) for x in y.split('\t') if len(x)>=1] for y in birth_data[1:] if len(y)>=1]      with open(birth_weight_file, 'w', newline='') as f:        writer=csv.writer(f)        writer.writerow(birth_header)        writer.writerows(birth_data)
把下载并经预处理的出生数据集读入内存：
  birth_data=[]   with open(birth_weight_file, newline='') as csvfile:      csv_reader=csv.reader(csvfile)      birth_header=next(csv_reader)      for row in csv_reader:        birth_data.append(row)      birth_data=[[float(x) for x in row] for row in birth_data]   # Pull out target variable   y_vals=np.array([x[0] for x in birth_data])   # Pull out predictor variables   x_vals=np.array([x[1:8] for x in birth_data])
分割数据集为测试集和训练集：
  train_indices=np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False)   test_indices=np.array(list(set(range(len(x_vals)))-set(train_indices)))   x_vals_train=x_vals[train_indices]   x_vals_test=x_vals[test_indices]   y_vals_train=y_vals[train_indices]   y_vals_test=y_vals[test_indices]
将所有特征缩放到0和1区间，成为归一化特征，这样逻辑回归收敛效果更好：
  def normalize_cols(m, col_min=np.array([None]), col_max=np.array([None])):      if not col_min[0]:        col_min=m.min(axis=0)      if not col_max[0]:        col_max=m.max(axis=0)      return (m-col_min)/(col_max-col_min), col_min, col_max   x_vals_train, train_min, train_max=np.nan_to_num(normalize_cols(x_vals_train))   x_vals_test, _, _=np.nan_to_num(normalize_cols(x_vals_test, train_min, train_max))
先分割数据集为测试集和训练集，然后再缩放，这样可以确保训练集和测试集互不影响。
然后声明批量大小、占位符、变量和逻辑模型：
  batch_size=25   x_data=tf.placeholder(shape=[None, 7],dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1],dtype=tf.float32)   A=tf.Variable(tf.random_normal(shape[7, 1]))   b=tf.Variable(tf.random_normal(shape[1, 1]))   model_output=tf.add(tf.matmul(x_data, A), b)
声明损失函数，其中包括sigmoid函数，并初始化变量，声明优化器：
  loss=tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(model_output, y_target))   init=tf.global_variables_initializer()   sess.run(init)   my_opt=tf.train.GradientDescentOptimizer(0.01)   train_step=my_opt.minimize(loss)
除了记录损失函数，还要记录分类器在训练集和测试集上的准确度，所以要创建一个返回准确度的预测函数：
  prediction=tf.round(tf.sigmoid(model_output))   prediction_correct=tf.cast(tf.equal(prediction, y_target), tf.float32)   accuracy=tf.reduce_mean(prediction_correct)
开始遍历迭代训练，记录损失值和准确度：
  loss_vec=[]   train_acc=[]   test_acc=[]   for i in range(1500):      rand_index=np.random.choice(len(x_vals_train), size=batch_size)      rand_x=x_vals_train[rand_index]      rand_y=np.transponse([y_vals_train[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      temp_loss=sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})      loss_vec.append(temp_loss)      temp_acc_train=sess.run(accuracy, feed_dict={x_data: x_vals_train, y_target: np.transpose([y_vals_train])})      train_acc.append(temp_acc_train)      temp_acc_test=sess.run(accuracy, feed_dict={x_data: x_vals_test, y_target: np.transpose([y_vals_test])})      test_acc.append(temp_acc_test)
绘制损失函数和准确度：
  plt.plot(loss_vec, 'k-')   plt.title('Cross Entropy Loss per Generation')   plt.xlabel('Generation')   plt.ylabel('Cross Entropy Loss')   plt.show()   plt.plot(train_acc, 'k-', label='Train Set Accuracy')   plt.plot(test_acc, 'r--', label='Test Set Accuracy')   plt.title('Train and Test Accuracy')   plt.xlabel('Generation')   plt.ylabel('Accuracy')   plt.legend(loc='lower right')   plt.show()
数据集只有189个观测值，因此训练集和测试集的准确度图由于数据集的随机分割将会变化。

4. 基于TensorFlow的支持向量机：

支持向量机算法是一种二值分类器方法，目标是找到两类之间的一个线性可分的直线或超平面，假定二分类目标是-1或1。有许多直线可以分割两类目标，定义分割两类目标有最大距离的直线为最佳线性分类器，公式Ax-b=0。其中，A是斜率向量，x是输入向量。最大间隔的宽度为2除以A的L2范数，从几何观点来看这是二维数据点到一条直线的垂直距离。
因为不是所有的数据集都是线性可分的，引入跨分割线的数据点的损失函数。对于n个数据点，引入soft margin损失函数：

如果数据点分割正确，乘积y_i(Ax_i-b)总是大于1，这意味着损失函数左边项等于0，这时对损失函数有影响的仅仅只有间隔大小。
上述损失函数寻求一个线性可分的直线，但是也允许有些点跨越间隔直线，这取决于a值。当a值很大，模型会倾向于尽量将样本分割开；a值越小，会有更多跨越边界的点存在。

1）线性支持向量机：

从iris数据集创建一个线性分类器，用花萼宽度和花萼长度特征预测是否为山鸢尾花。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   from sklearn import datasets
上面代码导入scikit learn的datasets库来访问iris数据集。然后创建计算图，加载iris数据集的第一列和第四列特征变量。加载特征变量时，山鸢尾花为1，否则为-1，代码为：
  sess=tf.Session()   iris=datasets.load_iris()   x_vals=np.array([[x[0], x[3]] for x in iris.data])   y_vals=np.array([1 if y==0 else -1 for y in iris.target])
分割数据集为训练集和测试集，并评估训练集和测试集训练的准确度：
  train_indices=np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False)   test_indices=np.array(list(set(range(len(x_vals)))-set(train_indices)))   x_vals_train=x_vals[train_indices]   x_vals_test=x_vals[test_indices]   y_vals_train=y_vals[train_indices]   y_vals_test=y_vals[test_indices]
设置批量大小、占位符和模型变量。对于支持向量机算法，希望用非常大的批量来帮助其收敛，小的批量会使得最大间隔线缓慢跳动。理想情况下，也应该缓慢减小学习率。A变量形状为2×1，因为有花萼长度和花萼宽度两个变量。代码为：
  batch_size=100   x_data=tf.placeholder(shape=[None, 2],dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1],dtype=tf.float32)   A=tf.Variable(tf.random_normal(shape[2, 1]))   b=tf.Variable(tf.random_normal(shape[1, 1]))
声明模型输出。对于正确分类的数据点，如果数据点是山鸢尾花，返回的数值大于或者等于1，否则返回的数值小于或者等于-1。代码：
  model_output=tf.subtract(tf.matmul(x_data, A), b)
声明最大间隔损失函数。首先声明一个函数来计算向量的L2范数，接着增加间隔参数a。声明分类器损失函数，并把前面两项加在一起。代码：
  l2_norm=tf.reduce_sum(tf.square(A))   alpha=tf.constant([0.1])   classification_term=tf.reduce_sum(tf.maximum(0., tf.subtract(1., tf.multiply(model_output, y_target))))   loss=tf.add(classification_term, tf.multiply(alpha, l2_norm))
声明预测函数和准确度函数，用来评估训练集和测试集的训练准确度：
  prediction=tf.sign(model_output)   accuracy=tf.reduce_sum(tf.cast(tf.equal(prediction, y_target), tf.float32))
声明优化器，并初始化模型变量：
  my_opt=tf.train.GradientDescentOptimizer(0.01)   train_step=my_opt.minimize(loss)   init=tf.global_variables_initializer()   sess.run(init)
开始遍历迭代训练模型，记录训练集和测试集训练的损失和准确度：
  test_accuracy=[]   for i in range(500):      rand_index=np.random.choice(len(x_vals_train), size=batch_size)      rand_x=x_vals_train[rand_index]      rand_y=np.transponse([y_vals_train[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      temp_loss=sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})      loss_vec.append(temp_loss[0])      train_acc_temp=sess.run(accuracy, feed_dict={x_data: x_vals_train, y_target: np.transponse([y_vals_train])})      train_accuracy.append(train_acc_temp)      test_acc_temp=sess.run(accuracy, feed_dict={x_data: x_vals_test, y_target: np.transponse([y_vals_test])})      test_accuracy.append(test_acc_temp)      if (i+1) % 100==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A))+' b='+str(sess.run(b)))        print('Loss='+str(temp_loss))
为了输出结果图，需要抽取系数，分割x_vals为山鸢尾I.setosa和非山鸢尾non-I.setosa：
  [[a1], [a2]]=sess.run(A)   [[b]]=sess.run(b)   slope=-a2/a1   y_intercept=b/a1   x1_vals=[d[1] for d in x_vals]   best_fit=[]   for i in x1_vals:      best_fit.append(slope*i+y_intercept)   setosa_x=[d[1] for i,d in in enumerate(x_vals) if y_vals[i]==1]   setosa_y=[d[0] for i,d in in enumerate(x_vals) if y_vals[i]==1]   not_setosa_x=[d[1] for i,d in in enumerate(x_vals) if y_vals[i]==-1]   not_setosa_y=[d[0] for i,d in in enumerate(x_vals) if y_vals[i]==-1]
绘制数据的线性分类器、准确度和损失图：
  plt.plot(setosa_x, setosa_y, 'o', label='I. setosa')   plt.plot(not_setosa_x, not_setosa_y, 'x', label='Non-setosa')   plt.plot(x1_vals, best_fit, 'r-', label='Linear Separator', linewidth=3)   plt.ylim([0, 10])   plt.legend(loc='lower right')   plt.title('Sepal Length vs Petal Width')   plt.xlabel('Petal Width')   plt.ylabel('Sepal Length')   plt.show()   plt.plot(train_accuracy, 'k-', label='Training Accuracy')   plt.plot(test_accuracy, 'r--', label='Test Accuracy')   plt.title('Training and Test Set Accuracies')   plt.xlabel('Generation')   plt.ylabel('Accuracy')   plt.legend(loc='lower right')   plt.show()   plt.plot(loss_vec, 'k-')   plt.title('Loss per Generation')   plt.xlabel('Generation')   plt.ylabel('Loss')   plt.show()
由于上面两类目标是线性可分的，得到的准确率为100%。
使用TensorFlow实现SVD算法可能导致每次运行的结果不尽相同，原因包括训练集和测试集的随机分割，每批训练的批量大小不同，理想情况下每次迭代后学习率缓慢减小。

2）弱化为线性回归：

支持向量机可以用来拟合线性回归。使用相同的iris数据集，进行花萼长度和花瓣宽度之间的线性拟合。损失函数类似于：
支持向量机拟合线性回归损失函数
其中，ε为间隔宽度的一半。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   from sklearn import datasets   sess=tf.Session()   iris=datasets.load_iris()   x_vals=np.array([x[3] for x in iris.data])   y_vals=np.array([y[0] for y in iris.data])   train_indices=np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False)   test_indices=np.array(list(set(range(len(x_vals)))-set(train_indices)))   x_vals_train=x_vals[train_indices]   x_vals_test=x_vals[test_indices]   y_vals_train=y_vals[train_indices]   y_vals_test=y_vals[test_indices]
声明批量大小、占位符和变量：
  batch_size=50   x_data=tf.placeholder(shape=[None, 1],dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1],dtype=tf.float32)   A=tf.Variable(tf.random_normal(shape[1, 1]))   b=tf.Variable(tf.random_normal(shape[1, 1]))   model_output=tf.add(tf.matmul(x_data, A), b)
声明损失函数，ε=0.5：
  epsilon=tf.constant([0.5])   loss=tf.reduce_mean(tf.maximum(0., tf.subtract(tf.abs(tf.subtract(model_output, y_target)), epsilon)))
创建优化器，初始化变量：
  my_opt=tf.train.GradientDescentOptimizer(0.075)   train_step=my_opt.minimize(loss)   init=tf.global_variables_initializer()   sess.run(init)
开始200次迭代训练，保存训练集和测试集损失函数：
  train_loss=[]   test_loss=[]   for i in range(200):      rand_index=np.random.choice(len(x_vals_train), size=batch_size)      rand_x=np.transponse([x_vals_train[rand_index]])      rand_y=np.transponse([y_vals_train[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      temp_train_loss=sess.run(loss, feed_dict={x_data: np.transponse([x_vals_train]), y_target: np.transponse([y_vals_train])})      train_loss.append(temp_train_loss)      temp_test_loss=sess.run(loss, feed_dict={x_data: np.transponse([x_vals_test]), y_target: np.transponse([y_vals_test])})      test_loss.append(temp_test_loss)      if (i+1) % 50==0:        print('Step #'+str(i+1)+'A='+str(sess.run(A))+' b='+str(sess.run(b)))        print('Train Loss='+str(temp_train_loss))        print('Test Loss='+str(temp_test_loss))
抽取系数，获得最佳拟合直线的截距，为了绘图，也获取间隔宽度值：
  [[slope]]=sess.run(A)   [[y_intercept]]=sess.run(b)   [[width]]=sess.run(epsilon)   slope=-a2/a1   best_fit=[]   best_fit_upper=[]   best_fit_lower=[]   for i in x_vals:      best_fit.append(slope*i+y_intercept)      best_fit_upper.append(slope*i+y_intercept+width)      best_fit_lower.append(slope*i+y_intercept-width)
绘制数据点和拟合曲线，以及训练集和测试集损失：
  plt.plot(x_vals, y_vals, 'o', label='Data Points')   plt.plot(x_vals, best_fit, 'r-', label='SVM Regression Line', linewidth=3)   plt.plot(x_vals, best_fit_upper, 'r--', linewidth=2)   plt.plot(x_vals, best_fit_lower, 'r--', linewidth=2)   plt.ylim([0, 10])   plt.legend(loc='lower right')   plt.title('Sepal Length vs Petal Width')   plt.xlabel('Petal Width')   plt.ylabel('Sepal Length')   plt.show()   plt.plot(train_loss, 'k-', label='Training Set Loss')   plt.plot(test_loss, 'r--', label='Test Set Loss')   plt.title('L2 Loss per Generation')   plt.xlabel('Generation')   plt.ylabel('L2 Loss')   plt.legend(loc='upper right')   plt.show()
直观地说，SVM回归算法试图把更多的数据点拟合到直线两边2ε宽度的间隔内。如果选择太小的ε值，SVM回归算法在间隔宽度内不能拟合更多的数据点；如果选择太大的ε，将有许多条直线能够在间隔宽度内拟合所有的数据点。一般更倾向于选取更小的ε值。

3）核函数的使用：

线性支持向量机问题的对偶表达式为：

其中：

上述表达式中，模型变量是向量b。在理想情况下，b向量是稀疏向量，iris数据集相关的支持向量仅仅取1和-1附近的值。数据点向量以x_i表示，目标值1或-1以y_i表示。
上面方程中的核函数是点积x_i·x_j，其为线性函数，该核函数是以数据点(i,j)的点积填充的方阵。替代数据点间的点积，可以将其扩展到更复杂的函数更高维度，需满足如下条件：

这里，k称为核函数。最广为人知的核函数之一是高斯核函数，也称径向基核函数或RBF核函数，描述方程：

为了用该核函数预测，假设观测数据点p_j，代入上述核函数中，得到：

示例中将用合适的线性核函数实现来替代上面的高斯核函数，使用程序生成的模拟数据。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   from sklearn import datasets   sess=tf.Session()
生成模拟数据。生成的数据是两个同心圆，每个不同的环代表不同的类，确保只有类1或-1.为了让绘图方便，将每类数据分成x值和y值。代码为：
  (x_vals, y_vals)=datasets.make_circles(n_samples=500, factor=.5, noise=.1)   y_vals=np.array([1 if y==1 else -1 for y in y_vals])   class1_x=[x[0] for i,x in enumerate(x_vals) if y_vals[i]==1]   class1_y=[x[1] for i,x in enumerate(x_vals) if y_vals[i]==1]   class2_x=[x[0] for i,x in enumerate(x_vals) if y_vals[i]==-1]   class2_y=[x[1] for i,x in enumerate(x_vals) if y_vals[i]==-1]
声明批量大小、占位符，创建模型变量b。对于SVM算法，为了让每次迭代训练不波动，得到一个稳定的训练模型，批量取值要大一些。为预测数据点还声明了额外的占位符，还创建彩色网格来可视化不同的区域代表不同的类别。代码：
  batch_size=250   x_data=tf.placeholder(shape=[None, 2],dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1],dtype=tf.float32)   prediction_grid=tf.placeholder(shape=[None, 2],dtype=tf.float32)   b=tf.Variable(tf.random_normal(shape[1, batch_size]))
创建高斯核函数，用矩阵操作来表示：
  gamma=tf.constant(-50.0)   dist=tf.reduce_sum(tf.square(x_data), 1)   dist=tf.reshape(dist, [-1,1])   sq_dists=tf.add(tf.subtract(dist, tf.multiply(2., tf.matmul(x_data, tf.transpose(x_data)))), tf.transpose(dist))   my_kernel=tf.exp(tf.multiply(gamma, tf.abs(sq_dists)))
其中，sq_dists中应用广播加法和减法操作。线性核函数可以表示为：
  my_kernel=tf.matmul(x_data, tf.transpose(x_data))
声明对偶问题，为了最大化，采用最小化损失函数的负数tf.neg()：
  model_output=tf.matmul(b, my_kernel)   first_term=tf.reduce_sum(b)   b_vec_cross=tf.matmul(tf.transpose(b), b)   y_target_cross=tf.matmul(y_target, tf.transpose(y_target))   second_term=tf.reduce_sum(tf.multiply(my_kernel, tf.multiply(b_vec_cross, y_target_cross)))   loss=tf.negative(tf.subtract(first_term, second_term))
创建预测函数和准确度函数。先创建一个预测核函数，但用预测数据点的核函数替代前面用模拟数据点的核函数。预测值是模拟输出的符号函数值。代码为：
  rA=tf.reshape(tf.reduce_sum(tf.square(x_data), 1), [-1,1])   rB=tf.reshape(tf.reduce_sum(tf.square(prediction_grid), 1), [-1,1])   pred_sq_dist=tf.add(tf.subtract(rA, tf.multiply(2., tf.matmul(x_data, tf.transpose(prediction_grid)))), tf.square(rB))   pred_kernel=tf.exp(tf.multiply(gamma, tf.abs(pred_sq_dist)))   prediction_output=tf.matmul(tf.multiply(tf.transpose(y_target), b), pred_kernel)   prediction=tf.sign(prediction_output-tf.reduce_mean(prediction_output))   accuracy=tf.reduce_mean(tf.cast(tf.equal(tf.squeeze(prediction), tf.squeeze(y_target)), tf.float32))
为了实现线性预测核函数，将预测核函数可改为：
  pred_kernel=tf.matmul(x_data, tf.transpose(prediction_grid))
创建优化器，初始化所有的变量：
  my_opt=tf.train.GradientDescentOptimizer(0.001)   train_step=my_opt.minimize(loss)   init=tf.global_variables_initializer()   sess.run(init)
开始迭代训练，记录每次迭代的损失向量和批量训练的准确度。计算准确度时，要为3个占位符赋值，其中x_data数据会被赋值两次来得到数据点的预测值。代码：
  loss_vec=[]   batch_accuracy=[]   for i in range(500):      rand_index=np.random.choice(len(x_vals), size=batch_size)      rand_x=x_vals[rand_index]      rand_y=np.transponse([y_vals[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      temp_loss=sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})      loss_vec.append(temp_loss)      acc_temp=sess.run(accuracy, feed_dict={x_data: rand_x, y_target: rand_y, prediction_grid: rand_x})      batch_accuracy.append(acc_temp)      if (i+1) % 100==0:        print('Step #'+str(i+1))        print('Loss='+str(temp_loss))
为了能够在整个数据空间可视化分类返回结果，将创建预测数据点的网格，并在其上进行预测，代码为：
  x_min, x_max=x_vals[:, 0].min()-1, x_vals[:, 0].max()+1   y_min, y_max=x_vals[:, 1].min()-1, x_vals[:, 1].max()+1   xx, yy=np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))   grid_points=np.c_[xx.ravel(), yy.ravel()]   [grid_predictions]=sess.run(prediction, feed_dict={x_data: x_vals, y_target: np.transpose([y_vals]), prediction_grid: grid_points)   grid_predictions=grid_predictions.reshape(xx.shape)
绘制预测结果、批量准确度和损失函数：
  plt.contourf(xx, yy, grid_predictions, cmap=plt.cm.Paired, alpha=0.8)   plt.plot(class1_x, class1_y, 'ro', label='Class 1')   plt.plot(class2_x, class2_y, 'kx', label='Class -1')   plt.legend(loc='lower right')   plt.xlim([-1.5, 1.5])   plt.ylim([-1.5, 1.5])   plt.show()   plt.plot(batch_accuracy, 'k-', label='Accuracy')   plt.title('Batch Accuracy')   plt.xlabel('Generation')   plt.ylabel('Accuracy')   plt.legend(loc='lower right')   plt.show()   plt.plot(loss_vec, 'k-')   plt.title('Loss per Generation')   plt.xlabel('Generation')   plt.ylabel('Loss')   plt.show()
对于一个新点的预测或者评估，可以使用以下命令：
  sess.run(prediction, feed_dict={x_data: x_vals, y_data: np.transpose([y_vals])})
该命令必须包含原始数据集x_vals和y_vals，原因在于SVM由支持向量定义，依据原始数据集明确新点在边缘或者不在边缘上。
高斯核函数能够分割非线性数据集，高斯核函数中有个参数gamma，控制数据集分割的弯曲部分的影响程度。一般情况下选择较小值，但也严重依赖于数据集，理想情况下，gamma值是通过统计技术来确定的，如交叉验证。
还有其他一些非线性核函数：
齐次多项式核函数：

非齐次多项式核函数：

双曲正切核函数：

4）实现非线性支持向量机：

加载iris数据集，使用高斯核函数SVM来分割，实现山鸢尾花分类器。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   from sklearn import datasets   sess=tf.Session()
加载iris数据集，抽取花萼长度和花瓣宽度，分割每类的x_vals值和y_vals值：
  iris=datasets.load_iris()   x_vals=np.array([[x[0], x[3]] for x in iris.data])   y_vals=np.array([1 if y==0 else -1 for y in iris.data])   class1_x=[x[0] for i,x in enumerate(x_vals) if y_vals[i]==1]   class1_y=[x[1] for i,x in enumerate(x_vals) if y_vals[i]==1]   class2_x=[x[0] for i,x in enumerate(x_vals) if y_vals[i]==-1]   class2_y=[x[1] for i,x in enumerate(x_vals) if y_vals[i]==-1]
声明批量大小、占位符和模型变量b：
  batch_size=100   x_data=tf.placeholder(shape=[None, 2],dtype=tf.float32)   y_target=tf.placeholder(shape=[None, 1],dtype=tf.float32)   prediction_grid=tf.placeholder(shape=[None, 2],dtype=tf.float32)   b=tf.Variable(tf.random_normal(shape[1, batch_size]))
声明高斯核函数，该核函数依赖gamma值：
  gamma=tf.constant(-10.0)   dist=tf.reduce_sum(tf.square(x_data), 1)   dist=tf.reshape(dist, [-1,1])   sq_dists=tf.add(tf.subtract(dist, tf.multiply(2., tf.matmul(x_data, tf.transpose(x_data)))), tf.transpose(dist))   my_kernel=tf.exp(tf.multiply(gamma, tf.abs(sq_dists)))
计算损失函数，解决双优化问题：
  model_output=tf.matmul(b, my_kernel)   first_term=tf.reduce_sum(b)   b_vec_cross=tf.matmul(tf.transpose(b), b)   y_target_cross=tf.matmul(y_target, tf.transpose(y_target))   second_term=tf.reduce_sum(tf.multiply(my_kernel, tf.multiply(b_vec_cross, y_target_cross)))   loss=tf.negative(tf.subtract(first_term, second_term))
为了使用SVM进行预测，创建一个预测核函数，然后声明一个准确度函数，其为正确分类的数据点的百分比：
  rA=tf.reshape(tf.reduce_sum(tf.square(x_data), 1), [-1,1])   rB=tf.reshape(tf.reduce_sum(tf.square(prediction_grid), 1), [-1,1])   pred_sq_dist=tf.add(tf.subtract(rA, tf.mul(2., tf.matmul(x_data, tf.transpose(prediction_grid)))), tf.transpose(rB))   pred_kernel=tf.exp(tf.multiply(gamma, tf.abs(pred_sq_dist)))   prediction_output=tf.matmul(tf.multiply(tf.transpose(y_target), b), pred_kernel)   prediction=tf.sign(prediction_output-tf.reduce_mean(prediction_output))   accuracy=tf.reduce_mean(tf.cast(tf.equal(tf.squeeze(prediction), tf.squeeze(y_target)), tf.float32))
声明优化器，初始化变量：
  my_opt=tf.train.GradientDescentOptimizer(0.01)   train_step=my_opt.minimize(loss)   init=tf.global_variables_initializer()   sess.run(init)
开始迭代训练，迭代300次，并保存损失值和批量准确度：
  loss_vec=[]   batch_accuracy=[]   for i in range(300):      rand_index=np.random.choice(len(x_vals), size=batch_size)      rand_x=x_vals[rand_index]      rand_y=np.transponse([y_vals[rand_index]])      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      temp_loss=sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})      loss_vec.append(temp_loss)      acc_temp=sess.run(accuracy, feed_dict={x_data: rand_x, y_target: rand_y, prediction_grid: rand_x})      batch_accuracy.append(acc_temp)
为了绘制决策边界Decision Boundary，创建一个数据点(x,y)的网格，评估预测函数：
  x_min, x_max=x_vals[:, 0].min()-1, x_vals[:, 0].max()+1   y_min, y_max=x_vals[:, 1].min()-1, x_vals[:, 1].max()+1   xx, yy=np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))   grid_points=np.c_[xx.ravel(), yy.ravel()]   [grid_predictions]=sess.run(prediction, feed_dict={x_data: x_vals, y_target: np.transpose([y_vals]), prediction_grid: grid_points)   grid_predictions=grid_predictions.reshape(xx.shape)
绘制决策边界的代码：
  plt.contourf(xx, yy, grid_predictions, cmap=plt.cm.Paired, alpha=0.8)   plt.plot(class1_x, class1_y, 'ro', label='I. setosa')   plt.plot(class2_x, class2_y, 'kx', label='Non-setosa')   plt.title('Gaussian SVM Results on Iris Data')   plt.xlabel('Petal Width')   plt.ylabel('Sepal Length')   plt.legend(loc='lower right')   plt.xlim([-0.5, 3.0])   plt.ylim([3.5, 8.5])   plt.show()
设置不同的gamma值1、10、25、100，会出现不同的结果图，gamma值越大，每个数据点对分类边界的影响就越大。

5）实现多类支持向量机：

用SVM也能分类多类目标，这里示例用iris数据集分类三种花。
SVM算法最初是为二值问题设计的，但是也可以通过一些策略进行多类的分类。主要策略有两种：一对多方法和一对一方法。
一对一方法是在任意两类样本之间设计创建一个二值分类器，然后得票最多的类别即为该未知样本的预测类别。但是当类别很多的时候，就必须创建k!/(k-2)!2!个分类器，计算的代价比较高。
一对多的方法是为每类创建一个分类器，最后的预测类别是具有最大SVM间隔的类别，本示例使用这种方法。
加载iris数据集，使用高斯核函数的非线性多类SVM模型。iris数据集含有3种鸢尾花，将创建3个高斯核函数SVM来预测。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   from sklearn import datasets   sess=tf.Session()
加载iris数据集并为每类分离目标值，因为想绘制结果图，只使用花萼长度和花瓣宽度两个特征，也分离x值和y值。代码：
  iris=datasets.load_iris()   x_vals=np.array([[x[0], x[3]] for x in iris.data])   y_vals1=np.array([1 if y==0 else -1 for y in iris.data])   y_vals2=np.array([1 if y==1 else -1 for y in iris.data])   y_vals3=np.array([1 if y==2 else -1 for y in iris.data])   y_vals=np.array([y_vals1, y_vals2, y_vals3])   class1_x=[x[0] for i,x in enumerate(x_vals) if y_vals[i]==0]   class1_y=[x[1] for i,x in enumerate(x_vals) if y_vals[i]==0]   class2_x=[x[0] for i,x in enumerate(x_vals) if y_vals[i]==1]   class2_y=[x[1] for i,x in enumerate(x_vals) if y_vals[i]==1]   class3_x=[x[0] for i,x in enumerate(x_vals) if y_vals[i]==2]   class3_y=[x[1] for i,x in enumerate(x_vals) if y_vals[i]==2]
数据集维度出现变化，从单目标分类到三类目标分类。利用矩阵传播和reshape技术一次性计算所有的三类SVM。由于一次性计算所有分类，y_target占位符的维度是[3, None]，模型变量b初始化大小为[3, batch_size]。代码：
  batch_size=50   x_data=tf.placeholder(shape=[None, 2],dtype=tf.float32)   y_target=tf.placeholder(shape=[3, None],dtype=tf.float32)   prediction_grid=tf.placeholder(shape=[None, 2],dtype=tf.float32)   b=tf.Variable(tf.random_normal(shape[3, batch_size]))
下面计算高斯核函数。因为核函数只依赖x_data，所以代码没有变化：
  gamma=tf.constant(-10.0)   dist=tf.reduce_sum(tf.square(x_data), 1)   dist=tf.reshape(dist, [-1,1])   sq_dists=tf.add(tf.subtract(dist, tf.multiply(2., tf.matmul(x_data, tf.transpose(x_data)))), tf.transpose(dist))   my_kernel=tf.exp(tf.multiply(gamma, tf.abs(sq_dists)))
最大的变化是批量矩阵乘法。因为最终结果是三维矩阵，并且需要传播矩阵乘法，所以数据矩阵和目标矩阵需要预处理，比如x^T·x操作需要额外增加一个维度，因此创建一个函数来扩展矩阵维度，然后进行矩阵转置，接着调用TensorFlow的tf.batch_matmul()函数。代码：
  def reshape_matmul(mat):      v1=tf.expand_dims(mat, 1)      v2=tf.reshape(v1, [3, batch_size, 1])      return tf.batch_matmul(v2, v1)
计算对偶损失函数：
  model_output=tf.matmul(b, my_kernel)   first_term=tf.reduce_sum(b)   b_vec_cross=tf.matmul(tf.transpose(b), b)   y_target_cross=reshape_matmul(y_target)   second_term=tf.reduce_sum(tf.multiply(my_kernel, tf.multiply(b_vec_cross, y_target_cross)), [1,2])   loss=tf.reduce_sum(tf.negative(tf.subtract(first_term, second_term)))
创建预测核函数，因为并不想聚合三个SVM预测，所以使用reduce_sum()函数时，需要通过第2个参数指明求和哪几个。代码：
  rA=tf.reshape(tf.reduce_sum(tf.square(x_data), 1), [-1,1])   rB=tf.reshape(tf.reduce_sum(tf.square(prediction_grid), 1), [-1,1])   pred_sq_dist=tf.add(tf.subtract(rA, tf.multiply(2., tf.matmul(x_data, tf.transpose(prediction_grid)))), tf.transpose(rB))   pred_kernel=tf.exp(tf.multiply(gamma, tf.abs(pred_sq_dist)))
创建预测函数，因为使用一对多方法，预测值是分类器有最大返回值的类别，使用TensorFlow的内建函数argmax()实现该功能。代码：
  prediction_output=tf.matmul(tf.mul(y_target, b), pred_kernel)   prediction=tf.argmax(prediction_output-tfexpand_dims(tf.reduce_mean(prediction_output, 1), 1), 0)   accuracy=tf.reduce_mean(tf.cast(tf.equal(prediction, tf.argmax(y_target, 0)), tf.float32))
声明优化器，并初始化变量：
  my_opt=tf.train.GradientDescentOptimizer(0.01)   train_step=my_opt.minimize(loss)   init=tf.global_variables_initializer()   sess.run(init)
该算法收敛很快，迭代次数不要超过100次。代码：
  loss_vec=[]   batch_accuracy=[]   for i in range(100):      rand_index=np.random.choice(len(x_vals), size=batch_size)      rand_x=x_vals[rand_index]      rand_y=y_vals[:, rand_index]      sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})      temp_loss=sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})      loss_vec.append(temp_loss)      acc_temp=sess.run(accuracy, feed_dict={x_data: rand_x, y_target: rand_y, prediction_grid: rand_x})      batch_accuracy.append(acc_temp)      if (i+1)%25==0:        print('Step #'+str(i+1))        print('Loss= '+str(temp_loss))
创建数据点预测网格，运行预测函数：
  x_min, x_max=x_vals[:, 0].min()-1, x_vals[:, 0].max()+1   y_min, y_max=x_vals[:, 1].min()-1, x_vals[:, 1].max()+1   xx, yy=np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))   grid_points=np.c_[xx.ravel(), yy.ravel()]   grid_predictions=sess.run(prediction, feed_dict={x_data: rand_x, y_target: rand_y, prediction_grid: grid_points)   grid_predictions=grid_predictions.reshape(xx.shape)
绘制训练结果、批量准确度和损失函数。训练结果绘制的代码：
  plt.contourf(xx, yy, grid_predictions, cmap=plt.cm.Paired, alpha=0.8)   plt.plot(class1_x, class1_y, 'ro', label='I. setosa')   plt.plot(class2_x, class2_y, 'kx', label='I. versicolor')   plt.plot(class3_x, class3_y, 'gv', label='I. virginica')   plt.title('Gaussian SVM Results on Iris Data')   plt.xlabel('Petal Length')   plt.ylabel('Sepal Width')   plt.legend(loc='lower right')   plt.xlim([-0.5, 3.0])   plt.ylim([3.5, 8.5])   plt.show()   plt.plot(batch_accuracy, 'k-', label='Accuracy')   plt.title('Batch Accuracy')   plt.xlabel('Generation')   plt.ylabel('Accuracy')   plt.legend(loc='lower right')   plt.show()   plt.plot(loss_vec, 'k-')   plt.title('Loss per Generation')   plt.xlabel('Generation')   plt.ylabel('Loss')   plt.show()
通过示例可以看到，使用TensorFlow内建功能，可以轻松扩展算法到多类。
一般来说，如果一个问题的训练集中有大量特征，建议用逻辑回归或者线性支持向量机算法；如果训练集的数量比较大，或者数据集是非线性可分的，建议使用带高斯核的支持向量机算法。

5. TensorFlow实现最近邻域法：

最近邻域法是先将训练集看作模型，然后基于新数据点与训练集的距离来预测新数据点，让预测值与最接近的训练数据集作为同一类。因为大部分样本数据包含一定程度的噪声，更通用的方法是用k个邻域的加权平均，称为k最近邻域法k-NN(k-nearest neighbor)。
假设样本训练集(x1,x2,...,xn)，对应目标值(y1,y2,...,yn)，通过最近邻域法预测数据点z。预测的实际方法取决于想做连续型的回归训练，还是离散型的分类训练。
对于离散型分类目标，预测值由到预测数据点的加权距离的最大值决定，公式：
离散型分类目标最近邻域法
其中，预测函数f(z)是所有分类j上的最大加权值；预测数据点到训练数据点i的加权距离用φ(d_ij)表示；I_ij是指示函数，表示数据点i是否属于分类j，当数据点i属于分类j时指示函数为1，否则为0；k是距离预测数据点最近的训练数据个数。
对于连续回归训练目标，预测值是所有k个最近邻域数据点到预测数据点的加权平均，公式：
连续回归训练目标最近邻域法
很明显，预测值非常依赖距离度量d方式的选择。常用的距离度量是L1范数和L2范数：
距离度量L1范数和L2范数
距离度量方式很多，也会使用编辑距离、文本距离等。
选择加权距离也有多种方法，最直观的是用距离本身来加权，考虑到更近的数据点对预测数据点的预测值影响应更小，因而最通用的加权方式是用距离的归一化倒数。
k-NN是一种聚类算法，对于回归算法来说，需要计算邻域的加权平均距离，因而预测值将比实际目标值的特征更平缓，影响的程度取决于k值，该值是算法中的邻域个数。

1）最近邻域法的使用：

最近邻域法用于房价预测，使用波士顿房价数据集训练，利用几个特征的函数来预测房价。使用Python的requests模块从UCI机器学习仓库加载波士顿房价数据集：
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   import requests   sess=tf.Session()
使用requests模块加载数据集：
  housing_url='https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data'   housing_header=['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']   cols_used=['CRIM', 'INDUS', 'NOX', 'RM', 'AGE', 'DIS', 'TAX', 'PTRATIO', 'B', 'LSTAT']   num_features=len(cols_used)   housing_file=requests.get(housing_url)   housing_data=[[float(x) for x in y.split(' ') if len(x)>=1] for y in housing_file.text.split('\n') if len(y)>=1]
分离数据集为特征依赖的数据集和特征无关的数据集，预测数据集中最后一个变量MEDV，该值为一组房价中的平均值。由于非相关特征或者二值特征，这里不使用ZN、CHAS、RAD这几个特征。代码：
  y_vals=np.transponse([np.array([y[13] for y in housing_data])])   x_vals=np.array([[x for i,x in enumerate(y) if housing_header[i] in cols_used] for y in housing_data])   x_vals=(x_vals-x_vals.min(0))/x_vals.ptp(0)
分离x_vals值和y_vals值为训练数据集和测试数据集。随机选择80%的行作为训练集，剩下的20%数据行作为测试集。代码：
  train_indices=np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False)   test_indices=np.array(list(set(range(len(x_vals)))-set(train_indices)))   x_vals_train=x_vals[train_indices]   x_vals_test=x_vals[test_indices]   y_vals_train=y_vals[train_indices]   y_vals_test=y_vals[test_indices]
声明k值和批量大小：
  k=4   batch_size=len(x_vals_test)
声明占位符。算法模型完全是通过训练集决定的，因此没有训练模型变量。代码：
  x_data_train=tf.placeholder(shape=[None, num_features],dtype=tf.float32)   x_data_test=tf.placeholder(shape=[None, num_features],dtype=tf.float32)   y_target_train=tf.placeholder(shape=[None, 1],dtype=tf.float32)   y_target_test=tf.placeholder(shape=[None, 1],dtype=tf.float32)
为批量测试集创建距离函数，使用L1范数距离：
  distance=tf.reduce_sum(tf.abs(tf.subtract(x_data_train, tf.expand_dims(x_data_test, 1))), reduction_indices=2)
如果使用L2范数距离，代码为：
  distance=tf.sqrt(tf.reduce_sum(tf.square(tf.sub(x_data_train, tf.expand_dims(x_data_test, 1))), reduction_indices=1))
创建预测函数。这里使用top_k()函数，以张量的方式返回最大值的值和索引。因为需要找到最小距离索引，所以对最大距离取负。声明预测函数和目标值的均方误差MSE。代码：
  top_k_xvals, top_k_indices=tf.nn.top_k(tf.negative(distance), k=k)   x_sums=tf.expand_dims(tf.reduce_sum(top_k_xvals, 1), 1)   x_sums_repeated=tf.matmul(x_sums, tf.ones([1, k], tf.float32))   x_sums_weights=tf.expand_dims(tf.divide(top_k_xvals, x_sums_repeated), 1)   top_k_yvals=tf.gather(y_target_train, top_k_indices)   prediction=tf.squeeze(tf.batch_matmul(x_val_weights, top_k_yvals), squeeze_dims=[1])   mse=tf.divide(tf.reduce_sum(tf.square(tf.subtract(prediction, y_target_test))), batch_size)
进行测试，对测试数据进行循环检验，存储预测值和准确度：
  num_loops=int(np.ceil(len(x_vals_test)/batch_size))   for i in range(num_loops):      min_index=i*batch_size      max_index=min((i+1)*batch_size, len(x_vals_train))      x_batch=x_vals_test[min_index:max_index]      y_batch=y_vals_test[min_index:max_index]      predictions=sess.run(prediction, feed_dict={x_data_train: x_vals_train, x_data_test: x_batch, y_target_train: y_vals_train, y_target_test: y_batch})      batch_mse=sess.run(mse, feed_dict={x_data_train: x_vals_train, x_data_test: x_batch, y_target_train: y_vals_train, y_target_test: y_batch})      print('Batch #'+str(i+1)+' MSE: '+str(np.round(batch_mse, 3)))   # Batch #1 MSE: 23.153
通过直方图来比较实际值和预测值：
  bins=np.linspace(5, 50, 45)   plt.hist(predictions, bins, alpha=0.5, label='Prediction')   plt.hist(y_batch, bins, alpha=0.5, label='Actual')   plt.title('Histogram of Predicted and Actual Values')   plt.xlabel('Med Home Value in $1,000s')   plt.ylabel('Frequency')   plt.legend(loc='upper right')   plt.show()
因为示例中使用的是平均方法，所以在预测目标值最大和最小值方面遇到问题。
算法中k的取值是个难点，这里选用k=4进行模型训练。选取该值，是通过交叉验证，其使得MSE最低。如果使用交叉验证来选取多个k值对比，可以看到k=4时MSE最小。也可以绘制预测值随k值变化的预测方差，显示出平均更多的邻域数据点时，预测方差会减小。
在最近邻域算法中，模型是训练数据集，因此训练模型中没有任何变量训练，只有一个参数k，通过交叉验证法最小化MSE来确定。

2）度量文本距离：

除了处理数据，最近邻域法还广泛应用于其他方面，只要有方法来度量距离，即可应用最近邻域算法。这里介绍度量文本距离。
文本距离度量可以使用字符串间的编辑距离Levenshtein距离，是指由一个字符串转换成另一个字符串所需要的最少编辑操作次数，允许的编辑操作包括插入一个字符、删除一个字符、将一个字符替换为另一个字符。这里使用TensorFlow的内建函数edit_distance()求解Levenshtein距离，这个函数仅仅接受稀疏张量，因此使用前需要将字符串转换成稀疏张量。
  import tensorflow as tf   sess=tf.Session()
计算两个英文单词间的编辑距离，用Python的list()函数创建字符列表，然后将列表映射为一个三维稀疏矩阵。TensorFlow的tf.SparseTensor()函数需指定字符索引、矩阵形状和张量中的非零值。在编辑距离计算时，指定normalize=False表示计算总的编辑距离；指定normalize =True表示计算归一化编辑距离，即通过编辑距离除以第2个单词的长度进行归一化。代码：
  hypothesis=list('bear')   truth=list('beers')   h1=tf.SparseTensor([[0,0,0],[0,0,1],[0,0,2],[0,0,3]], hypothesis, [1,1,1])   t1=tf.SparseTensor([[0,0,0],[0,0,1],[0,0,1],[0,0,3],[0,0,4]], truth, [1,1,1])   print(sess.run(tf.edit_distance(h1, t1, normalize=False)))   # [[2.]]
TensorFlow把两个字符串处理为参考字符串hypothesis和真实字符串truth，代码中标记为h张量和t张量。
如果比较两个单词bear和beer与另一个单词beers。代码为：
  hypothesis2=list('bearbeer')   truth2=list('beersbeers')   h2=tf.SparseTensor([[0,0,0],[0,0,1],[0,0,2],[0,0,3],[0,1,0],[0,1,1],[0,1,2],[0,1,3]], hypothesis2, [1,2,4])   t2=tf.SparseTensor([[0,0,0],[0,0,1],[0,0,2],[0,0,3],[0,0,4],[0,1,0],[0,1,1],[0,1,2],[0,1,3],[0,1,4]], truth2, [1,2,5])   print(sess.run(tf.edit_distance(h2, t2, normalize=True)))   # [[0.40000001 0.2]]
更有效地比较一个单词集合与单个单词的方法，需要先为参考字符串和真实字符串创建索引和字符列表。代码：
  hypothesis_words=['bear', 'bar', 'tensor', 'flow']   truth_word=['beers']   num_h_words=len(hypothesis_words)   h_indices=[[xi, 0, yi] for xi,x in enumerate(hypothesis_words) for yi,y in enumerate(x)]   h_chars=list(''.join(hypothesis_words))   h3=tf.SparseTensor(h_indices, h_chars, [num_h_words,1,1])   thuth_word_vec=truth_word*num_h_words   t_indices=[[xi, 0, yi] for xi,x in enumerate(thuth_word_vec) for yi,y in enumerate(x)]   t_chars=list(''.join(truth_word_vec))   t3=tf.SparseTensor(t_indices, t_chars, [num_h_words,1,1])   print(sess.run(rf.edit_distance(h3, t3, normalize=True)))   # [[0.40000001] [0.60000002] [0.80000001] [1.]]
可以使用占位符来计算两个单词列表之间的编辑距离，使用SparseTensorValue()替代稀疏张量。首先创建一个函数，根据单词列表输出稀疏张量：
  def create_sparse_vec(word_list):      num_words=len(word_list)      indices=[[xi, 0, yi] for xi,x in enumerate(word_list) for yi,y in enumerate(x)]      chars=list(''.join(word_list))      return (tf.SparseTensorValue(indices, chars, [num_words, 1, 1]))   hyp_string_sparse=create_sparse_vec(hypothesis_words)   truth_string_sparse=create_sparse_vec(truth_word*len(hypothesis_words))   hyp_input=tf.sparse_placeholder(dtype=tf.string)   truth_input=tf.sparse_placeholder(dtype=tf.string)   edit_distances=tf.edit_distance(hyp_input, truth_input, normalize=True)   feed_dict={hyp_input: hyp_string_sparse, truth_input: truth_string_sparse}   print(sess.run(edit_distances, feed_dict=feed_dict))
文本度量有几种方式：
  ·  汉明距离(Hamming distance)：两个等长字符串中对应位置的不同字符串的个数
文本度量汉明距离
其中，I为等长字符串的指示函数。
  ·  余弦距离(Cosine distance)：不同k-gram的点积除以不同k-gram的L2范数
文本度量余弦距离
  ·  Jaccard距离(Jaccard distance)：两个字符串中相同字符数除以所有字符数
文本度量Jaccard距离

3）实现混合距离计算：

当处理的数据观测点有多种特征时，要意识到不同的特征应该用不同的归一化方式来缩放。
加权距离函数使用加权权重矩阵，包含矩阵操作的距离函数表达式为：
包含矩阵操作的加权距离函数表达式
其中，A为对角权重矩阵，用来对每个特征的距离度量进行调整。
使用波士顿房价数据集的MSE，该数据集的特征维度不同，因此缩放后的距离函数对使用最近邻域法有利。
  import matplotlib.pyplot as plt   import numpy as np   import tensorflow as tf   import requests   sess=tf.Session()
加载数据集，存为numpy数组，不使用id变量或方差非常小的变量。代码：
  housing_url='https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data'   housing_header=['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']   cols_used=['CRIM', 'INDUS', 'NOX', 'RM', 'AGE', 'DIS', 'TAX', 'PTRATIO', 'B', 'LSTAT']   num_features=len(cols_used)   housing_file=requests.get(housing_url)   housing_data=[[float(x) for x in y.split(' ') if len(x)>=1] for y in housing_file.text.split('\n') if len(y)>=1]   y_vals=np.transponse([np.array([y[13] for y in housing_data])])   x_vals=np.array([[x for i,x in enumerate(y) if housing_header[i] in cols_used] for y in housing_data])
用min-max缩放法缩放x值到0和1之间：
  x_vals=(x_vals-x_vals.min(0))/x_vals.ptp(0)
创建对角权重矩阵，提供归一化距离度量，其值为特性的标准差：
  weight_diagonal=x_vals.std(0)   weight_matrix=tf.cast(tf.diag(weight_diagonal), dtype=tf.float32)
分割数据集为训练集和测试集，声明k值，该值为最近邻域的数量，设置批量大小为测试集大小：
  train_indices=np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False)   test_indices=np.array(list(set(range(len(x_vals)))-set(train_indices)))   x_vals_train=x_vals[train_indices]   x_vals_test=x_vals[test_indices]   y_vals_train=y_vals[train_indices]   y_vals_test=y_vals[test_indices]   k=4   batch_size=len(x_vals_test)
声明占位符，有4个，分别是训练集和测试集的x值输入和y目标输入：
  x_data_train=tf.placeholder(shape=[None, num_features],dtype=tf.float32)   x_data_test=tf.placeholder(shape=[None, num_features],dtype=tf.float32)   y_target_train=tf.placeholder(shape=[None, 1],dtype=tf.float32)   y_target_test=tf.placeholder(shape=[None, 1],dtype=tf.float32)
声明距离函数，为可读性将距离函数分解，需要tf.tile函数为权重矩阵指定batch_size维度扩展，使用batch_matmul()函数进行批量矩阵乘法。代码：
  subtraction_term=tf.subtract(x_data_train, tf.expand_dims(x_data_test, 1))   first_product=tf.batch_matmul(subtraction_term, tf.tile(tf.expand_dims(weight_matrix, 0), [batch_size, 1, 1]))   second_product=tf.batch_matmul(first_product, tf.transponse(subtraction_term, perm=[0, 2, 1]))   distance=tf.sqrt(tf.batch_matrix_diag_part(second_product))
计算完每个测试数据点的距离，需要使用tf.nn.top_k()函数返回k-NN法的前k个最近邻域。因为返回的为最大值，而需要的是最小距离，因此转换成返回距离负值的最大值。然后将前k个最近邻域的距离进行加权平均做预测。代码：
  top_k_xvals, top_k_indices=tf.nn.top_k(tf.neg(distance), k=k)   x_sums=tf.expand_dims(tf.reduce_sum(top_k_xvals, 1), 1)   x_sums_repeated=tf.matmul(x_sums, tf.ones([1, k], tf.float32))   x_sums_weights=tf.expand_dims(tf.div(top_k_xvals, x_sums_repeated), 1)   top_k_yvals=tf.gather(y_target_train, top_k_indices)   prediction=tf.squeeze(tf.batch_matmul(x_val_weights, top_k_yvals), squeeze_dims=[1])
计算预测值的MSE，评估训练模型：
  mse=tf.divide(tf.reduce_sum(tf.square(tf.subtract(prediction, y_target_test))), batch_size)
遍历迭代训练批量测试数据，每次迭代计算其MSE：
  num_loops=int(np.ceil(len(x_vals_test)/batch_size))   for i in range(num_loops):      min_index=i*batch_size      max_index=min((i+1)*batch_size, len(x_vals_train))      x_batch=x_vals_test[min_index:max_index]      y_batch=y_vals_test[min_index:max_index]      predictions=sess.run(prediction, feed_dict={x_data_train: x_vals_train, x_data_test: x_batch, y_target_train: y_vals_train, y_target_test: y_batch})      batch_mse=sess.run(mse, feed_dict={x_data_train: x_vals_train, x_data_test: x_batch, y_target_train: y_vals_train, y_target_test: y_batch})      print('Batch #'+str(i+1)+' MSE: '+str(np.round(batch_mse, 3))) # Batch #1 MSE: 21.322
为了对比，绘制测试数据集的房价分布和测试集上的预测值的分布：
  bins=np.linspace(5, 50, 45)   plt.hist(predictions, bins, alpha=0.5, label='Prediction')   plt.hist(y_batch, bins, alpha=0.5, label='Actual')   plt.title('Histogram of Predicted and Actual Values')   plt.xlabel('Med Home Value in $1,000s')   plt.ylabel('Frequency')   plt.legend(loc='upper right')   plt.show()
通过对特征的距离进行缩放，减小测试数据集的MSE。代码中使用的是特征的标准差因子来缩放距离函数，并且对top k邻域进行加权平均作为距离函数来进行房价预测。
缩放因子可以加强或者减弱最近邻域距离计算中特征的权重，这样更符合实际特征的作用。

4）实现地址匹配：

最近邻域应用在地址匹配上是非常有效的。地址匹配中，地址中有许多打印错误，但是都指向同一个地址，使用最近邻域算法综合地址信息的数值部分和字符部分可以帮助鉴定实际相同的地址。这是一个结合数值距离和文本距离来度量包含文本特征又包含数值特征的数据观测点间距离的实例。
  import random   import string   import numpy as np   import tensorflow as tf
创建数据集，为了简洁每个数据集仅由10个地址组成：
  n=10   street_names=['abbey', 'baker', 'canal', 'donner', 'elm']   street_types=['rd', 'st', 'ln', 'pass', 'ave']   rand_zips=[random.randint(65000,65999) for i in range(5)]   numbers=[random.randint(1, 9999) for i in range(n)]   streets=[random.choice(street_names) for i in range(n)]   street_suffs=[random.choice(street_types) for i in range(n)]   zips=[random.choice(rand_zips) for i in range(n)]   full_streets=[str(x)+' '+y+' '+z for x,y,z in zip(numbers, streets, street_suffs)]   reference_data=[list(x) for x in zip(full_streets, zips)]
为了创建一个测试数据集，需要一个随机创建“打印错误”的字符串函数，返回结果字符串：
  def create_typo(s, prob=0.75):      if random.uniform(0,1)<prob:        rand_ind=random.choice(range(len(s)))        s_list=list(s)        s_list[rand_ind]=random.choice(string.ascii_lowercase)        s=''.join(s_list)        return s   typo_streets=[create_typo(x) for x in streets]   typo_full_streets=[str(x)+' '+y+' '+z for x,y,z in zip(numbers, typo_streets, street_suffs)   test_data=[list(x) for x in zip(typo_full_streets, zips)]
初始化计算图，声明占位符。需要4个占位符，每个测试集和参考集需一个地址和邮政编码占位符。代码：
  sess=tf.Session()   test_address=tf.sparse_placeholder(dtype=tf.string)   test_zip=tf.placeholder(shape=[None, 1], dtype=tf.float32)   ref_address=tf.sparse_placeholder(dtype=tf.string)   ref_zip=tf.placeholder(shape=[None, n], dtype=tf.float32)
声明数值的邮政编码距离和地址字符串的编辑距离：
  zip_dist=tf.square(tf.subtract(ref_zip, test_zip)   address_dist=tf.edit_distance(test_address, ref_address, normalize=True)
把邮政编码距离和地址距离转换成相似度。当两个输入完全一致时，相似度为1；当它们完全不一致时为0。对于邮政编码，计算方式为：最大邮政编码减去该邮政编码，然后除以邮政编码范围，即最大邮政编码减去最小邮政编码的差值。对于地址相似度，其值已经是0和1之间的值，所以直接用1减去其编辑距离大小。代码为：
  zip_max=tf.gather(tf.squeeze(zip_dist), tf.argmax(zip_dist, 1))   zip_min=tf.gather(tf.squeeze(zip_dist), tf.argmin(zip_dist, 1))   zip_sim=tf.divide(tf.subtract(zip_max, zip_dist), tf.subtract(zip_max, zip_min))   address_sim=tf.subtract(1., address_dist)
结合上面的两个相似度函数，并对其进行加权平均。这里把地址和邮政编码的权重设为相等，各为0.5，也可以根据每个特征来调整权重，然后返回参考集最大相似度的索引。代码为：
  address_weight=0.5   zip_weight=1.-address_weight   weighted_sim=tf.add(tf.transpose(tf.multiply(address_weight, address_sim)), tf.multiply(zip_weight, zip_sim))   top_match_index=tf.argmax(weighted_sim, 1)
为了在TensorFlow中使用编辑距离，必须把地址字符串转换成稀疏向量。以自定义转换函数进行稀疏矩阵的转换。代码为：
  def sparse_from_word_vec(word_vec):      num_words=len(word_vec)      indices=[[xi, 0, yi] for xi,x in enumerate(word_vec) for yi,y in enumerate(x)]      chars=list(''.join(word_vec))      return (tf.SparseTensorValue(indices, chars, [num_words, 1, 1]))
分离参考集中的地址和邮政编码，然后在遍历迭代训练中为占位符赋值：
  reference_addresses=[x[0] for x in reference_data]   reference_zips=np.array([[x[1] for x in reference_data]])
利用自定义函数将参考地址转换成稀疏矩阵：
  sparse_ref_set=sparse_from_word_vec(reference_addresses)
遍历测试集的每一项，返回参考集中最接近项的索引，打印出测试集和参考集的每项：
  for i in range(n):      test_address_entry=test_data[i][0]      test_zip_entry=[[test_data[i][1]]]      test_address_repeated=[test_address_entry]*n      sparse_test_set=sparse_from_word_vec(test_address_repeated)      feeddict={test_address: sparse_test_set, test_zip: test_zip_entry, ref_address: sparse_ref_set, ref_zip: reference_zips}      best_match=sess.run(top_match_index, feed_dict=feeddict)      best_street=reference_addresses[best_match[0]]      [best_zip]=reference_zips[0][best_match]      [[test_zip_]]=test_zip_entry      print('Address: '+str(test_address_entry)+', '+str(test_zip_))      print('Match: '+str(best_street)+', '+str(best_zip))
解决地址匹配问题时会遇到很多困难，比如权重大小和如何归一化距离，这些都得根据实际数据选择解决方法。处理数值地址部分时，可以将其看成数字或者字符，取决于怎样选择。如果考虑到人为输入或者电脑输入错误，也可以用编辑距离函数来处理邮政编码。

5）实现图像识别：

最近邻域算法也常用于图像识别。MNIST手写数字样本数据集由上万张28×28像素已标注的图片组成，包含784个特征可供最近邻域算法训练，选用k=4的最近k邻域模型。
  import random   import numpy as np   import tensorflow as tf   import matplotlib.pyplot as plt   from PIL import Image   from tensorflow.examples.tutorials.mnist import input_data
创建一个计算图会话，加载MNIST手写数字数据集，并指定one-hot编码：
  sess=tf.Session()   mnist=input_data.read_data_sets("MNIST_data/", one_hot=True)
one-hot编码是分类类别的数值化，这样更有利于后续的数值计算。本例有10个类别，采用长度为10的0-1向量表示。
由于MNIST数据集较大，直接计算成千上万个输入的784个特征之间的距离比较困难，所以抽样为小数据集进行训练。对测试集也进行抽样处理，为了绘图方便，选择测试集数量可以被6整除，最后绘制6张图片查看效果。代码为：
  train_size=1000   test_size=102   rand_train_indices=np.random.choice(len(mnist.train.images), train_size, replace=False)   rand_test_indices=np.random.choice(len(mnist.test.images), test_size, replace=False)   x_vals_train=mnist.train.images[rand_train_indices]   x_vals_test=mnist.train.images[rand_test_indices]   y_vals_train=mnist.train.labels[rand_train_indices]   y_vals_test=mnist.train.labels[rand_test_indices]
声明k值和批量大小：
  k=4   batch_size=6
初始化占位符并赋值：
  x_data_train=tf.placeholder(shape=[None, 784], dtype=tf.float32)   x_data_test=tf.placeholder(shape=[None, 784], dtype=tf.float32)   y_target_train=tf.placeholder(shape=[None, 10], dtype=tf.float32)   y_target_test=tf.placeholder(shape=[None, 10], dtype=tf.float32)
声明距离度量函数，这里使用L1范数（绝对值）作为距离函数：
  distance=tf.reduce_sum(tf.abs(tf.subtract(x_data_train, tf.expand_dims(x_data_test, 1))), reduction_indices=2)
如果使用L2范数，代码为：
  distance=tf.sqrt(tf.reduce_sum(tf.square(tf.sub(x_data_train, tf.expand_dims(x_data_test, 1))), reduction_indices=1))
找到最接近的top k图片和预测模型。在数据集的one-hot编码索引上进行预测模型计算，然后统计发生的数量，最终预测为数量最多的类别。代码为：
  top_k_xvals, top_k_indices=tf.nn.top_k(tf.negative(distance), k=k)   prediction_indices=tf.gather(y_target_train, top_k_indices)   count_of_predictions=tf.reduce_sum(prediction_indices, reduction_indices=1)   prediction=tf.argmax(count_of_predictions)
在测试集上遍历迭代运行，计算预测值，并将结果存储：
  num_loops=int(np.ceil(len(x_vals_test)/batch_size))   test_output=[]   actual_vals=[]   for i in range(num_loops):      min_index=i*batch_size      max_index=min((i+1)*batch_size, len(x_vals_train))      x_batch=x_vals_test[min_index:max_index]      y_batch=y_vals_test[min_index:max_index]      predictions=sess.run(prediction, feed_dict={x_data_train: x_vals_train, x_data_test: x_batch, y_target_train: y_vals_train, y_target_test: y_batch})      test_output.extend(predictions)      actual_vals.extend(np.argmax(y_batch, axis=1))
计算模型准确度，此值会因为测试数据集和训练数据集的随机抽样而变化，但准确度约为80~90%。代码为：
  accuracy=sum([1./test_size for i in range(test_size) if test_output[i]==actual_vals[i]])   print('Accuracy on test set: '+str(accuracy))   # Accuracy on test set: 0.833333333333
绘制最后批次的计算结果：
  actuals=np.argmax(y_batch, axis=1)   Nrows=2   Ncols=3   for i in range(len(actuals)):      plt.subplot(Nrows, Ncols, i+1)      plt.imshow(np.reshape(x_batch[i], [28, 28]), cmap='Greys_r')      plt.title('Actual: '+str(actuals[i])+' Pred: '+str(predictions[i]), fontsize=10)      frame=plt.gca()      frame.axes.get_xaxis().set_visible(False)      frame.axes.get_yaxis().set_visible(False)
如果有足够的计算时间和计算资源，可以让训练数据集和测试数据集足够大，那么该方法可以增加准确度，这也是预防过拟合的普通方法之一。最近邻域算法中k的选择一般是通过在数据集上进行交叉验证获得。

5. TensorFlow用于其他机器学习算法：

TensorFlow也可以用来实现任意表示为计算图的迭代算法。

1）实现遗传算法：

遗传算法是最优化参数空间的有效方法，基本思想是创建一个随机初始化的种群，进化、重组和突变生成新的种群，通过当前种群的个体适应度来计算各个个体的适应度。
一般来说，遗传算法的大体步骤为：先随机初始化种群，通过各个个体的适应度排序，选择适应度较高的个体随机重组（或者交叉）创建下一代种群。下一代种群经过轻微变异产生不同于上一代的更好的适应度，然后将其放入父种群，在对子种群和父种群进行组合后，重复前面的整个过程。
遗传算法停止迭代的标准很多，这里仅以迭代的总次数为标准，也可以以在当前种群个体适应度达到预期的标准，或者在许多次迭代后最大的适应度不再变化时停止迭代。
这里将生成一个最接近ground truth函数：

的个体，其中包含50个浮点数数组。适应度为个体和ground truth函数的均方误差的负值。
  import os   import numpy as np   import matplotlib.pyplot as plt   import tensorflow as tf
设置遗传算法的参数。有100个个体，每个长度为50，选择的百分比是20%，即适应度排序前20的个体。变异定义为特征数的倒数，意味着下一代种群的一个特征会变异。运行遗传算法迭代200次，代码为：
  pop_size=100   features=50   selection=0.2   mutation=1./features   generations=200   num_parents=int(pop_size*selection)   num_children=pop_size-num_parents
初始化计算图会话，创建ground truth函数，该函数用来计算适应度：
  sess=tf.Session()   truth=np.sin(2*np.pi*(np.arange(features, dtype=float32))/features)
使用随机正态分布初始化种群：
  population=tf.Variable(np.random.randn(pop_size, features), dtype=float32)
创建遗传算法的占位符，是为ground truth函数和每次迭代改变的数据而创建，因为希望父代变化和变异概率变化交叉，这些都是模型的占位符。代码：
  truth_ph=tf.placehoulder(tf.float32, [1, features])   crossover_mat_ph=tf.placeholder(tf.float32, [num_children, features])   mutation_val_ph=tf.placeholder(tf.float32, [num_children, features])
计算群体的适应度，即均方误差的负值，选择较高适应度的个体：
  fitness=-tf.reduce_mean(tf.square(tf.subtract(population, truth_ph)), 1)   top_vals, top_ind=tf.nn.top_k(fitness, k=pop_size)
为了获得最后的结果并绘图，希望检索种群中适应度最高的个体：
  best_val=tf.reduce_min(top_vals)   best_ind=tf.argmin(top_vals, 0)   best_individual=tf.gather(population, best_ind)
排序父种群，截取适应度较高的个体作为下一代：
  population_sorted=tf.gather(population, top_ind)   parents=tf.slice(population_sorted, [0,0], [num_parents, features])
通过创建两个随机shuffle的父种群矩阵来创建下一代种群。将交叉矩阵分别与1和0相加，然后与父种群矩阵相乘，生成每一代的占位符。代码为：
  # Indices to shuffle-gather parents   rand_parent1_ix=np.random.choice(num_parents, num_children)   rand_parent2_ix=np.random.choice(num_parents, num_children)   # Gather parents by shuffled indices, expand back out to pop_size too   rand_parent1=tf.gather(parents, rand_parent1_ix)   rand_parent2=tf.gather(parents, rand_parent2_ix)   rand_parent1_sel=tf.multiply(rand_parent1, tf.subtract(1., crossover_mat_ph))   rand_parent2_sel=tf.multiply(rand_parent2, tf.subtract(1., crossover_mat_ph))   children_after_sel=tf.add(rand_patent1_sel, rand_patent2_sel)
最后一个步骤是变异下一代，这里将增加一个随机正常值到下一代种群矩阵中，然后将这个矩阵和父种群连接：
  mutated_children=tf.add(children_after_sel, mutation_val_ph)   # Combine children and parents into new population   new_population=tf.concat(0, [parents, mutated_children])
模型最后一步是使用group()操作分配下一代种群到父一代种群的变量：
  step=tf.group(population.assign(new_population))
初始化模型变量：
  init=tf.global_variables_initializer()   sess.run(init)
迭代训练模型，再创建随机交叉矩阵和变异矩阵，更新每代的种群：
  for i in range(generations):      # Create cross-over matrices for plugging in      crossover_mat=np.ones(shape=[num_children, features])      crossover_point=np.random.choice(np.arange(1, features-1, step=1), num_children)      for pop_ix in range(num_children):        crossover_mat[pop_ix, 0:corssover_point[pop_ix]]=0.      # Generate mutation probability matrices      mutation_prob_mat=np.random.uniform(size=[num_children, features])      mutation_values=np.random_normal(size=[num_children, features])      mutation_values[mutation_prob_mat>=mutation]=0      # Run GA step      feed_dict={truth_ph: truth.reshape([1, features]), crossover_mat_ph: crossover_mat, matation_val_ph: mutation_values}      step.run(feed_dict, session=sess)      best_individual_val=sess.run(best_individual, feed_dict=feed_dict)      if i%5==0:        best_fit=sess.run(best_val, feed_dict=feed_dict)        print('Generation: {}, Best Fitness (lowest MSE): {:, 2}'.format(i, -best_fit))
部分输出结果：
  Generation: 185, Best Fitness (lowest MSE): 0.085   Generation: 190, Best Fitness (lowest MSE): 0.15   Generation: 195, Best Fitness (lowest MSE): 0.083
为了验证实现的遗传算法是否工作，绘出每次迭代适应度最高的个体和ground truth趋势图，可以看出适应度最高的个体和ground truth相当接近。
遗传算法有很多变种，可以有两个父种群和两个不同的适应度标准，如最低MSE和平滑度，能强制变异值不大于1或者不小于-1。对于大部分遗传算法，计算适应度是一种艰难的任务，比如使用遗传算法优化神经网络架构，那么群体个体就有一个参数数组，参数包括过滤器大小、步长以及卷积层。对于数据集来说，迭代固定次数后，个体的适应度是分类的准确度，如果种群中有100个个体，那么每次迭代必须评估100个不同的CNN模型，这是非常大强度的计算。在使用遗传算法解决问题之前，需要考虑多久才能计算完个体的适应度，如果该操作很耗时，则不适合使用遗传算法。

2）实现k-means聚类算法：

TensorFlow是解决有监督模型的机器学习算法的理想工具，但也可以实现无监督模型，比如用来实现迭代聚类算法k-means。这里使用iris数据集，将数据聚类为三组，然后和实际标注比较求出聚类的准确度。
  import numpy as np   import matplotlib.pyplot as plt   import tensorflow as tf   from sklearn import datasets   from scipy.spatial import cKDTree   from sklearn.decomposition import PCA   from sklearn.preprocessing import scale
为了将四维的结果数据转换为二维数据进行可视化，因此要从sklearn库导入PCA工具。
创建一个计算图，加载iris数据集：
  sess=tf.Session()   iris=datasets.load_iris()   num_pts=len(iris.data)   num_feats=len(iris.data[0])
设置分类数、迭代次数，创建计算图所需的变量：
  k=3   generation=25   data_points=tf.Variable(iris.data)   cluster_labels=tf.Variable(tf.zeros([num_pts], dtype=tf.int64))
声明每个分组所需的几何中心变量，通过随机选择iris数据集中的3个数据点来初始化k-means聚类算法的几何中心：
  rand_starts=np.array([iris.data[np.random.choice(len(iris.data))], for _ in range(k)])   centroids=tf.Variable(rand_starts)
计算每个数据点到每个几何中心的距离，这里将几何中心点和数据点分别放入矩阵中，然后计算两个矩阵的欧式距离：
  centroids_matrix=tf.reshape(tf.tile(centroids, [num_pts, 1]), [num_pts, k, num_feats])   points_matrix=tf.reshape(tf.tile(data_points, [1, k]), [num_pts, k, num_feats])   distance=tf.reduce_sum(tf.square(point_matrix-centroid_matrix), reduction_indices=2)
分配时是以到每个数据点最小距离为最接近的几何中心点：
  centroid_group=tf.argmin(distances, 1)
计算每组分类的平均距离得到新的几何中心点：
  def data_group_avg(group_ids, data):      # Sum each group      sum_total=tf.unsorted_segment_sum(data, group_ids, 3)      # Count each group      num_total=tf.unsorted_segment_sum(tf.ones_like(data), group_ids, 3)      # Calculate average      avg_by_group=sum_total/num_total      return(avg_by_group)   means=data_group_avg(centroid_group, data_points)   update=tf.group(centroids.assogn(means), cluster_labels.assign(centroid_group))
初始化模型变量：
  init=tf.global_variables_initializer()   sess.run(init)
遍历迭代训练，相应地更新每组分类的几何中心点：
  for i in range(generations):      print('Calculating gen {}, out of {}.'.format(i, generations))      _, centroid_group,_count=sess.run([update, centroid_group])      group_count=[]      for ix in range(k):        group_count.append(np.sum(centroid_group_count==ix))      print('Group counts: {}'.format(group_count))
部分输出结果：
  Calculating gen 1, out of 25. Group counts: [50, 35, 65]   Calculating gen 24, out of 25. Group counts: [50, 38, 62]
为了验证聚类模型，使用距离模型预测，计算有多少数据点与实际iris数据集中的鸢尾花品种匹配：
  [centers, assignments]=sess.run([centroids, cluster_labels])   def most_common(my_list):      return(max(set(my_list), key=my_list.count))   label0=most_common(list(assignments[0:50]))   label1=most_common(list(assignments[50:100]))   label2=most_common(list(assignments[100:150]))   group0_count=np.sum(assignments[0:50]==label0)   group1_count=np.sum(assignments[50:100]==label1)   group2_count=np.sum(assignments[100:150]==label2)   accuracy=(group0_count+group1_count+group2_count)/150.   print('Accuracy: {: .2}'.format(accuracy))   # Accuracy: 0.89
为了可视化分组过程，以及是否分离出鸢尾花品种，将用PCA工具将四维结果数据转为二维结果数据，并绘制数据点和分组。PCA分解后创建预测，并在x-y轴网格绘制彩色图形。代码为：
  pca_model=PCA(n_components=2)   reduced_data=pca_model.fit_transform(iris.data)   reduced_centers=pca_model.transform(centers)   # Step size of mesh for plotting   h=.02   x_min, x_max=reduced_data[:, 0].min()-1, reduced_data[:, 0].max()+1   y_min, y_max=reduced_data[:, 1].min()-1, reduced_data[:, 1].max()+1   xx, yy=np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))   # Get k-means classifications for the grid points   xx_pt=list(xx.ravel())   yy_pt=list(yy.ravel())   xy_pts=np.array([[x,y] for x,y in zip(xx_pt, yy_py)])   my_tree=cKDTree(reduced_centers)   dist, indexes=mytree.query(xy_pts)   indexes=indexes.reshape(xx.shape)
用matplotlib模块在同一幅图形中绘制所有结果的代码，按照scikit-learn官方文档示例，网址http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_digits.html。代码：
  plt.clf()   plt.imshow(indexes, interpolation='nearst', extent=(xx.min(), xx.max(), yy.min(), yy.max()), cmap=plt.cm.Paired, aspect='auto', origin='lower')   # Plot each of the true iris data groups   symbols=['o', '^', 'D']   label_name=['Setosa', 'Versicolour', 'Virginica']   for i in range(3):      temp_group=reduced_data[(i*50):(50)*(i+1)]      plt.plot(temp_group[:, 0], temp_group[:, 1], symbols[i], markersize=10, label=label_name[i])   # Plot the centroids as a white X   plt.scatter(reduced_centers[:, 0], reduced_centers[:, 1], marker='x', s=169, linewidths=3, color='w', zorder=10)   plt.title('K-means clustering on Iris Datasets' 'Centroids are marked with white cross')   plt.xlim(x_min, x_max)   plt.ylim(y_min, y_max)   plt.legend('lower right')   plt.show()
图中会显示三种阴影区域，三种不同的数据点是三个鸢尾花品种。
上面示例是使用TensorFlow将iris数据集聚类为3组，然后计算数据点落入分组的百分比，绘制k-means分组的图形。因为k-means算法为分类算法的一种，为局部线性，所以很难学习到杂色鸢尾花versicolour和维吉尼亚鸢尾花virginica之间的非线性边界，但这种k-means算法的优点是无须标注数据集。

3）求解常微分方程：

求解一个常微分方程数值解是一个很容易用计算图表达的迭代过程，这里求解洛特卡-沃尔泰拉(Lotka-Volterra)掠食者-猎物方程组，此方程组用来描述生物系统中掠食者与猎物关系的动态模型。方程组离散数学表达式为：

其中，X是猎物，Y是掠食者。是通过a、b、c、d的值来决定哪个是猎物，哪个是掠食者，对于猎物，a>0，b<0；对于掠食者，c<0，d>0。使用TensorFlow实现其离散版的求解器。
  import matplotlib.pyplot as plt   import tensorflow as tf   sess=tf.Session()
声明计算图中的常量和变量：
  x_initial=tf.constant(1.0)   y_initial=tf.constant(1.0)   X_t1=tf.Variable(x_initial)   Y_t1=tf.Variable(y_initial)   t_delta=tf.placeholder(tf.float32, shape=())   a=tf.placeholder(tf.float32, shape=())   b=tf.placeholder(tf.float32, shape=())   c=tf.placeholder(tf.float32, shape=())   d=tf.placeholder(tf.float32, shape=())
实现掠食者-猎物方程组，然后更新X和Y：
  X_t2=X_t1+(a*X_t1+b*X_t1*Y_t1)*t_delta   Y_t2=Y_t1+(c*Y_t1+d*X_t1*Y_t1)*t_delta   step=tf.group(X_t1.assign(X_t2), Y_t1.assign(Y_t2))
初始化计算图，运行离散常微分方程，用指定参数说明周期性变化：
  init=tf.global_variables_initializer()   sess.run(init)   prey_values=[]   predator_values=[]   for i in range(1000):      # Step simulation (using constants for a known cyclic solution)      step.run({a: (2./3.), b: (-4./3.), c: -1.0, d: 1.0, t_delta: 0.01}, session=sess)      # Store each outcome      temp_prey, temp_pred=sess.run([X_t1, Y_t1])      prey_values.append(temp_prey)      predator_values.append(temp_pred)
获得洛特卡-沃尔泰拉方程组的稳定求解与指定参数和起始值有很大关系，可以通过尝试不同的参数和初始值比较结果。
绘制掠食者与猎物的值：
  plt.plot(prey_values, label="Prey")   plt.plot(pred_values, label="Predator")   plt.legend(loc='upper right')   plt.show()
通过绘制的图可以看到，掠食者与猎物的生态系统是周期变化的。

4）实现随机森林算法：

随机森林算法集成了多个决策树，决策树的观测值和特征值都是有可能随机选择的，这里给出使用梯度提升来训练的随机森林类型，用TensorFlow来计算。
基于树的算法传统上是非平滑的，因为是对数据进行分区来最小化目标输出中的方差，非平滑方法不适合基于梯度的方法。TensorFlow的使用依赖以下条件，模型中使用的函数是平滑的，并且它自动计算如何更改模型参数以最小化函数损失。克服这个缺陷的方式是对决策边界进行平滑逼近，可以使用softmax函数或类似形状的函数来逼近决策边界。
决策树通过生成规则对数据集进行硬拆分，如x>0.5，则移动到树的这个分支，数据子集是组合在一起还是拆分取决于x的值。而对决策树的平滑逼近处理是用概率，数据集的每次观测都有一定概率存在于树的每个末端节点中，形成概率决策树。
TensorFlow包含了一些默认模型估计函数，两个主要的梯度提升模型是回归树和分类树，这里使用回归树来预测波士顿房屋价格数据集。
  import numpy as np   import tensorflow as tf   from keras.datasets import boston_housing   from tensorflow.python.framework import ops   ops.reset_default_graph()
从TensorFlow估计库中设置要使用的模型，这里使用BoostedTreesRegressor模型，该模型用于使用梯度提升树的回归。代码为：
  regression_classifier=tf.estimator.BoostedTreesRegressor
对于二值分类问题，可以使用BoostedTreesClassifier估计器，目前不支持多类分类，或者将来会支持。
使用Keras数据导入函数加载波士顿房屋价格数据集：
  (x_train, y_train), (x_test, y_test)=boston_housing.load_data()
设置一些模型参数。批量大小是一次迭代的训练数据数量，将进行500次迭代训练，梯度提升森林有100棵树，每棵树最大深度为6。代码：
  batch_size=32   train_steps=500   n_trees=100   max_depth=6
为模型估计器创建数据输入函数，但首先需要将数据放入正确标记的numpy数组格式字典中，称为特征列。将数字列放入自动存储桶中，二值特征具有两个存储桶，连续数字特征将被划分为5个存储桶。代码为：
  binary_split_cols=['CHAS', 'RAD']   col_names=['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']   X_dtrain={col: x_train[:, ix] for ix,col in enumerate(col_names)}   X_dtest={col: x_test[:, ix] for ix,col in enumerate(col_names)}   # Create feature columns   feature_cols=[]   for ix,column in enumerate(x_train.T):      col_name=col_names[ix]      # Create binary split feature      if col_name in binary_split_cols:        # To create 2 buckets, need 1 boundary - the mean        bucket_boundaries=[column.mean()]        numeric_feature=tf.feature_column.numeric_column(col_name)        final_feature=tf.feature_column.bucketized_column(source_column=numeric_feature, boundaries=bucket_boundaries)        # Create bucketed feature      else:        # To create 5 buckets, need 4 boundaries        bucket_boundaries=list(np.linspace(column.min()*1.1, column.max()*0.9, 4))        numeric_feature=tf.feature_column.numeric_column(col_name)        final_feature=tf.feature_column.bucketized_column(source_column=numeric_feature, boundaries=bucket_boundaries)      # Add feature to feature_col list      feature_cols.append(final_feature)
最好将输入函数的shuffle选项设为True进行训练，设置为False进行测试，每个epoch都对X和Y训练集进行shuffle，但测试期间不shuffle。
使用估计器的输入库中的numpy输入函数来声明数据输入函数，指定创建的训练观测词典和一组y目标：
  input_fun=tf.estimator.inputs.numpy_input_fn(X_dtrain, y=y_train, batch_size=batch_size, num_epochs=10, shuffle=True)
声明模型并开始训练：
  model=regression_classifier(feature_columns=feature_cols, n_trees=n_trees, max_depth =max_depth, learning_rate=0.25, n_batches_per_layer=batch_size)   model.train(input_fn=input_fun, steps=train_steps)
为了评估模型，为测试数据创建另一个输入函数，并获得每个测试数据点的预测。以下代码能获取预测并打印平均绝对误差MAE：
  p_input_fun=tf.estimator.inputs.numpy_input_fn(X_dest, y=y_test, batch_size=batch_size, num_epochs=1, shuffle=False)   # Get predictions   predictions=list(model.predict(input_fn=p_input_fun))   final_preds=[pred['predictions'][0] for pred in predictions]   # Get accuracy (mean absolute error, MAE)   mae=np.mean([np.abs((actual-predicted)/predicted) for actual, predicted in zip(y_test, final_preds)])   print('Mean Abs Err on test set: {}'.format(mae)) # Mean Abs Err on test set: 0.7111111111111
MAE大约为0.71。由于shuffle具有随机性，可能会得到略微不同的结果。为了提高准确度，可以考虑增加epoch或引入更低的学习率，甚至是某种类型的缩减学习率，如指数形或线性。

赵工的个人空间

（专业技术部分）（转网页计算）（转业余爱好部分）