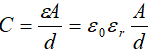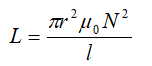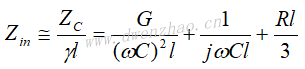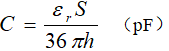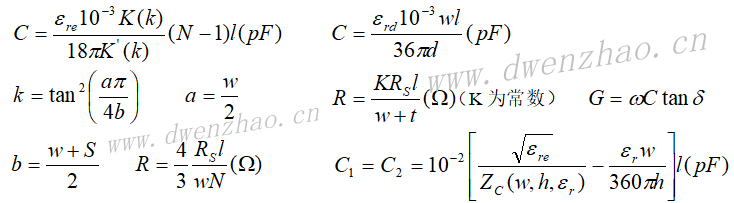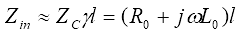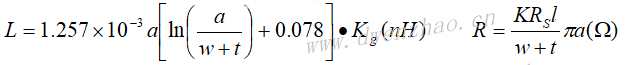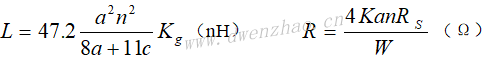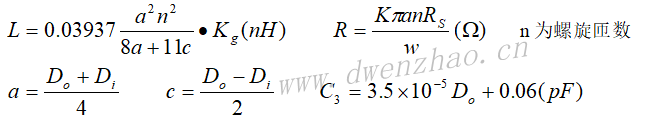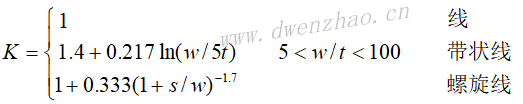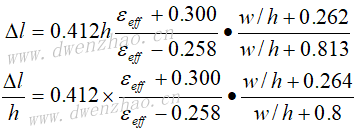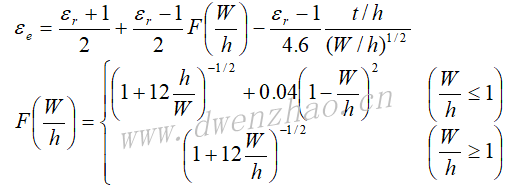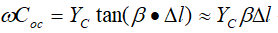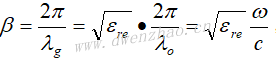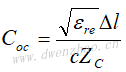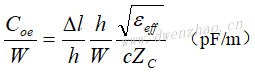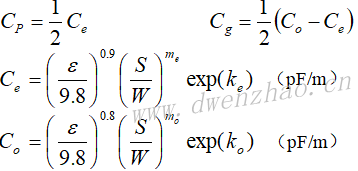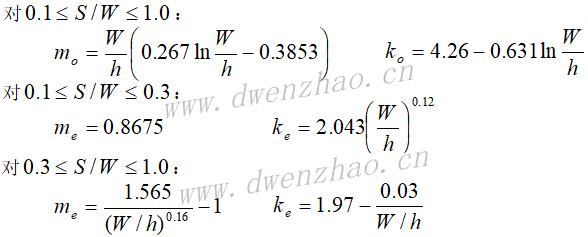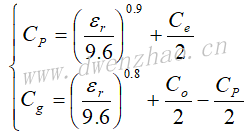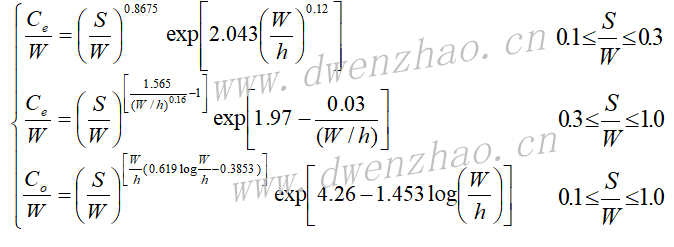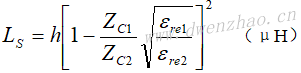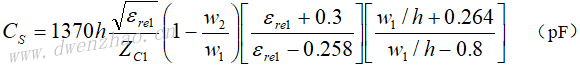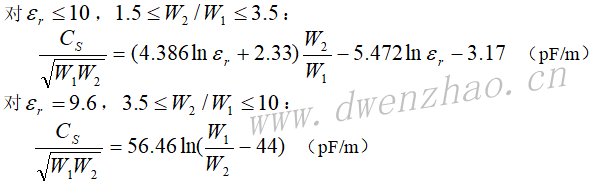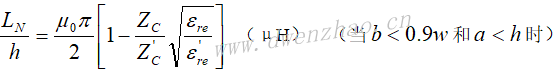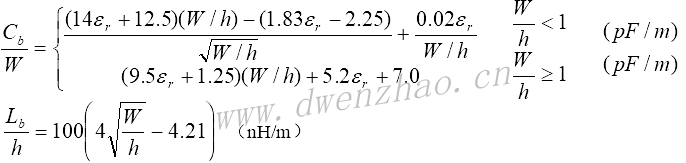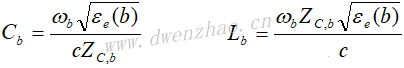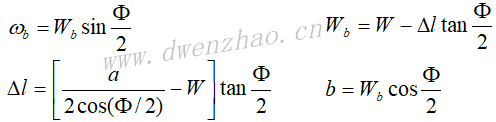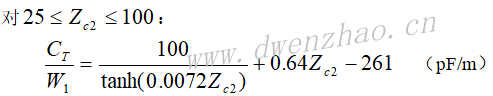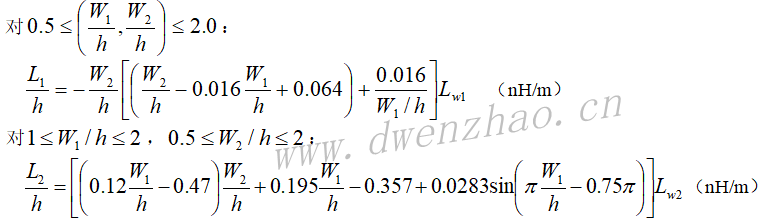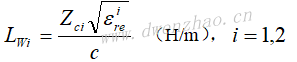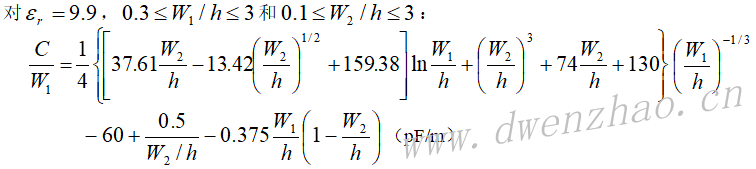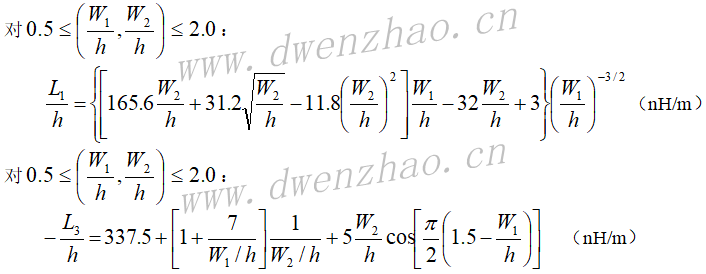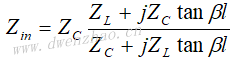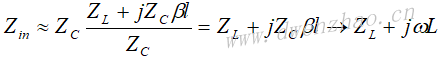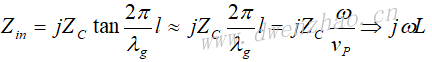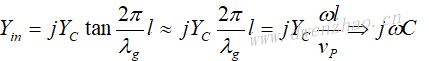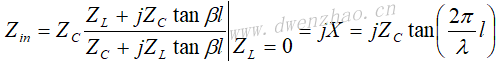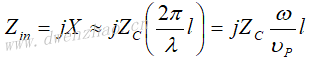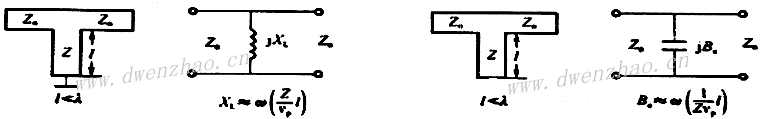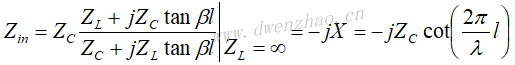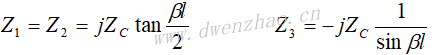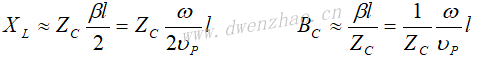赵工的个人空间

元器件高频模型及微带元件

1. 高频应用时的电阻、电容和电感等效电路：
• 电阻器的高频等效模型：
• 电容器的高频等效模型：
• 电感器的高频等效模型：
2. MMIC中使用的集总元件：
• 集总电阻器：
• 集总电容器：
• 集总电感器：
3. 微带不连续处的分布参数：
• 微带线的截断：
• 微带线的串联间隙：
• 微带线的对称阶梯：
• 微带线的开槽：
• 微带线的弯折：
• 微带线的T形接头：
• 微带线的十字接头：
• 高低阻抗传输线：
• 短路短截线：
• 开路短截线：
4. 微带线构成的电容和电感：
• 并联电感和并联电容的实现：
• 串联电感和并联电容的实现：
• 高低阻抗线等效电路：
• 串联电容的实现：

低频电路中经常要用到电阻、电容、电感等电子元器件，但这些实际器件在高频使用时会出现一些分布参数特性，不再是单纯的电阻、电容或电感，一般要用等效模型来描述其特性。而到了微波频段，往往不能使用集总参数的电阻、电容或电感，而要使用一些特殊结构的元器件来等效。

1. 高频应用时的电阻、电容和电感等效电路：

1）电阻器的高频等效模型：

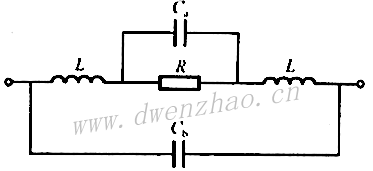
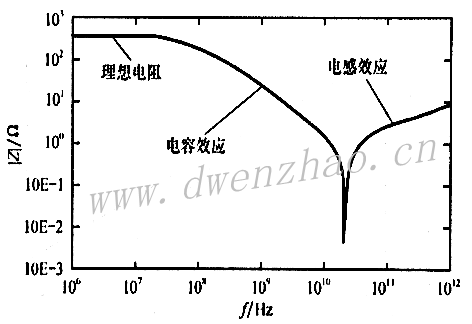
电阻器是电子线路中最常用的基础元件之一，常用于构成分压电路提供器件的直流偏置，也可用作负载电阻来完成某些特定功能。电阻器的高频等效电路见下图：

高频应用时，电阻元件不仅具有电阻值，还会有引线电感和线间寄生电容。C_a为电阻引脚间的等效电容，C_b表示引线间电容，L为引线电感。
实际的电阻元件有多种类型，但为了使引线电感尽量小，高频应用一般都应使用薄膜片式电阻，因为绕线电阻还具有线间电容且等效电感也较大，因此高频应用较少使用绕线电阻。

上图是某型号的500Ω金属膜电阻的频率特性曲线。可以看出，在低频率下阻抗即等于电阻R，而随着频率的升高达到10MHz以上，电容C_a的影响开始占优，导致总阻抗降低；当频率达到20GHz左右时，出现并联谐振点；越过并联谐振点后引线电感的影响开始表现出来，阻抗又加大并逐渐表现为开路或有限阻抗值。 可见，实际电阻元件在高频应用时已不再仅是一个电阻器，而是因多种分布参数的影响而表现出其他特性，在微波应用时这种效应更加明显，往往需要查相关厂商的电阻特性曲线来进行选择和使用。

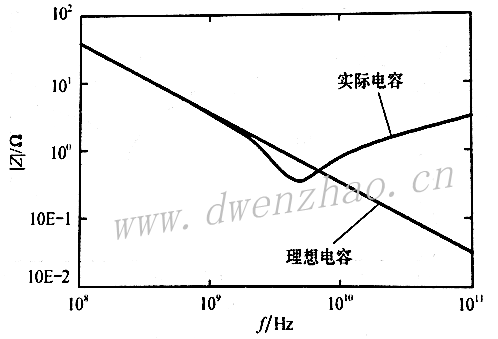
2）电容器的高频等效模型：

在低频率下，电容器一般都可以看成平行板结构，其极板的尺寸要远大于极板间距离，理想状态下极板间介质中没有电流。电容量定义为：

式中，A为极板面积，d表示极板间距离，ε=ε₀ε_r为极板填充介质的介电常数。
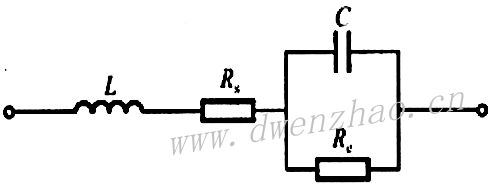
在高频下，实际的介质并非理想介质，因此介质内部存在传导电流，也即存在传导电流引起的损耗，更重要的是介质中的带电粒子具有一定的质量和惯性，在电磁场作用下很难随之振荡，导致在时间上有滞后现象，也会引起对能量的损耗。 高频应用时，要考虑引线电感L、引线导体损耗的串联电阻R_S和介质损耗电阻R_e，因此电容器的高频等效电路见下图：

一个47pF电容器，填充介质Al₂O₃的损耗角正切为10^-4，其阻抗的频率特性曲线为：

可以看出，在高频段其特性已经偏离理想电容很多，当损耗角正切本身还是频率的函数时其特性变异将更严重。

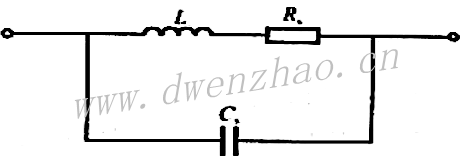
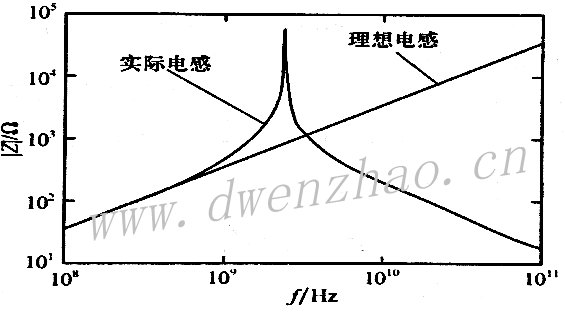
3）电感器的高频等效模型：

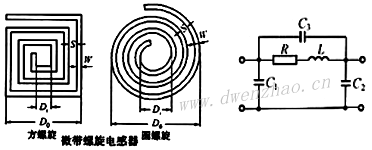
电子线路中常用的电感器一般是线绕结构，在高频下也称为高频扼流圈，结构一般是用直导线沿柱状结构缠绕而成。导线的缠绕构成电感的主要部分，而导线本身的电感可以忽略不计，细长螺线管的电感量为：

式中，r为螺线管半径，N为圈数，l为螺线管长度。在考虑了匝间电容C_S以及引线导体损耗的串联电阻R_S后，电感等效电路为：

对一个3.5圈的铜绕线电感，半径为1.27mm，长度为1.27mm，导线半径63.5um，可求出电感部分为61.4nH。因两螺线间距d=l/N=3.6×10^-4mm，可得到极板面积A=2al_wire=2a(2πrN)，其中l_wire为绕成线圈的导线总长度，得0.087pF。 导线的自身阻抗为0.034Ω。其特性阻抗的频率特性曲线为：

可以看出，这一铜电感线圈的高频特性已经完全不同于理想电感。在谐振点之前其阻抗升高很快，而在谐振点以后，由于寄生电容的影响已经逐步处于优势地位而逐渐减小。

2. MMIC中使用的集总元件：

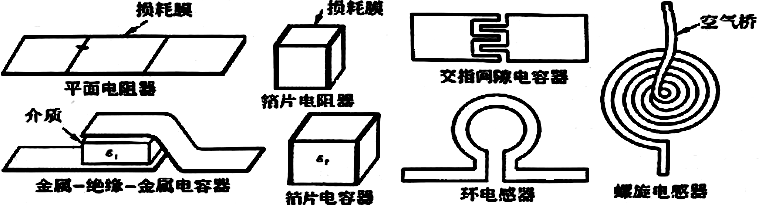
设计射频微波集成电路MMIC时也会使用集总元件时，但要考虑到构造它们的线长要甚小于波长，一般要小于传输信号波长的十分之一。一些常用的集总参数元件结构见下图：

1）集总电阻器：

平面电阻器可以用有耗物质（例如镍铬合金、氮化钽及掺杂半导体等）在一陶瓷基板上沉积一薄膜层（厚度从0.05~0.5μm）而成。这种芯片可以弯曲或焊接在MMIC电路上。可用下式近似计算：

式中，R_S为表面电阻（Ω/单位面积），σ为薄膜的电阻率（Ω·m），而d、W和l分别是薄膜的厚度、宽度和长度，以m计。当薄膜厚度≥1um时，应使用R_S计算R；而对于厚度≤1um的薄膜，则应使用σ来计算R。
好的电阻器的性能包括稳定的电阻值、低的温度系数、良好的散热能力、最大的长度小于0.1λ_g和低的寄生参数。由于存在杂散电容及分布电感使得其特性与频率有关。

2）集总电容器：

集总电容器可以认为是一个长度很短的开路线。当γl<<1和G<<ωC时，可得：

微带线介质基片上的小导体片与接地板之间就构成了一个电容器，在混合微波集成电路中，也采用单独的高介电常数的绝缘材料作基片，在基片两面敷银形成电容器的两个电极并以银带作引出线而构成片状微型电容器。微带片状电容器的电容量可以用平板电容器的公式来计算：

式中，S为电容器导体片（极板）面积；h为介质基片厚度；ε_r为介质基片的介电常数。尺寸单位mm。
简单方式也可以用边缘耦合或顶端耦合方式来形成电容：

微带片状电容器容量一般都很小（<0.2pF）。

利用交指结构一般可以获得小于1pF的电容值，其制造工艺简单，直接将微带线的导体带刻蚀成交叉指形状就可以形成，其等效电容如上面左图。当电路中要求电容器具有更大电容值时，可以采用薄膜电容器，结构如右图。 薄膜电容器由金属-氧化物-金属薄膜组成，金属薄膜的厚度应当达2～4倍趋肤深度（在2GHz频率上大约为4～8μm），氧化物作为电容器金属电极之间的绝缘介质，常采用S_iO₂或S_iN₂，其厚度为0.05～1μm。
交指结构平面电容器和薄膜电容器的计算公式为（尺寸为um）：

N为交叉指的条数；ε_re为宽度W的微带线的有效介电常数；ε_rd是氧化物薄膜的介电常数，tanδ则为其损耗角正切；Z_C为微带线特性阻抗；h、ε_r分别为介质基片的厚度与介电常数，K(k)为第一类完全椭圆积分。式中尺寸单位mm。 第一类椭圆积分的比值前面已经提到，K(k)/K(k')的误差小于3X10-6的近似表达式为： 共面波导

3）集总电感器：

可以用一段很短的终端短路线来模拟，其输入阻抗为：

如图是常用电感器的计算公式及其等效电路（尺寸为um）。
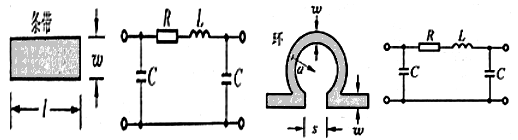
带状电感器：由微带线的一段直导体带构成，如上面左图。其单位长度的电感量和单位长度的电阻为：

t为导体带的厚度，一般来说，相对于W，t可以忽略不计。式中R_S为导体带的表面电阻率，单位为欧/正方形面积（Ω/□），其中f为工作频率，μ为导体带材料的导磁率，ρ为导体带材料的电阻率（导电率的倒数），K是考虑到电感器导体角上电流密集的修正因子。
由L、R即可求出电感器的无载品质因数（固有品质因数）：Q=ωL/R
环形电感器：如上面中图。其电感量和电阻分别是：

式中a的单位um。
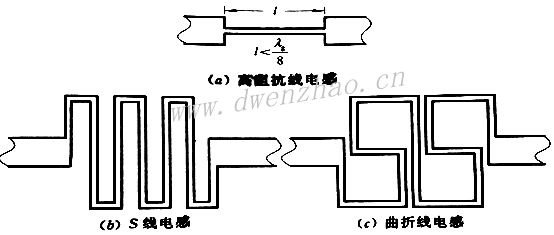
也可以使用高阻抗线和曲折线来形成电感：

螺旋电感器：主要有方螺旋和圆螺旋两种形式。其结构和等效电路为：

方螺旋的电感量和电阻计算公式为（单位mm）：

圆螺旋的电感量和电阻计算公式为（单位um）：

D₀为螺旋的外径，D_i为螺旋的内径；n为螺旋的匝数；S为螺旋各圈之间的间距，W为螺旋导体带宽度。
设计螺旋电感器时，线间距离s应尽可能小，而电感器的直径应小于λ/30以避免分布参数效应，通常也要求一空气桥或介质覆盖层以连接线圈内圈的端头。
由于地面的影响，使电感器的电感量减小，这种影响可以引入修正因数来计算：L=K_gL₀，其中L₀为电感器在自由空间中的电感量，K_g为计入地面等的影响后的修正因子。
带状线的修正因子为：K_g=0.57-0.154ln(w/h)      (w/h>0.05)
式中，w是线的宽度，h是衬底的厚度。作为第一次近似，上式也可用于其它型式电感器。MMIC中电感器的典型值为0.2~10nH。
为了计算电感器的Q值而需先决定导体的高额电阻值，可用公式计算：R=KR_Sl
式中，R_S是每单位导体板的电阻，l为长度，K是计入电感器导体在转弯处电流积聚的影响后的修正因子。对几种结构的K值为：

式中，t是导体厚度，w是线宽，s是螺旋线的间距。
引线电感：上面给出的电感量计算公式中，考虑了地面对电感量的影响，引入了修正因子K_g。而当微带电路需要与有源器件连接时，或者与输入输出插脚连接时，都会使用到引线，作为引线的导线将会给微带电路引入一个附加电感量。直径为d和长度为l（单位mm）的导线在自由空间的电感量L（单位nH）和电阻R（单位Ω）为：

3. 微带不连续处的分布参数：

微带线是常用的平面传输线，微带线的截断、导带宽度的突变以及微带线的分支等在微波电路中很常见，这种不连续性往往会带来一些分布参数，其中一些参数可以定量计算。

1）微带线的截断：

微带线的截断是指微带线导体带的终断，但并不代表微带线的开路，因为在导体带终断处场发生畸变，出现过剩电荷及与其相关的过剩电流，同时还有一定能量辐射。因此，微带线的截断实际上相当于一个RLC终端，R代表能量辐射损耗，L代表过剩电流，C代表过剩电荷。 但是，实际上当微带线工作于1GHz以下时，截断终端的辐射损耗和过剩电流都可以忽略不计，即使在1GHz以上的频率下，等效网络中仍以电容C起主要作用；另外，微带线中的介质基板的厚度达到一定程度时，单纯的电容等效截断也会引起较大误差，好在实际上介质基板的厚度一般总是远小于工作波长。 这样一来，在一般情况下，微带线的截断就可以等效成一个电容负载C_OC。根据长线理论，这个电容负载可以相当于一小段理想开路线，或者说将微带线实际截断处延伸一段距离Δl_OC，就等效为真正的开路端，反之在设计微带线开路端时就应将微带线的实际长度缩短Δl_OC。Δl_OC的大小可以根据经验公式求出：

式中，w为导带宽度，h为衬底高度，ε_eff为等效相对介电常数。ε_eff计算公式为：

其中，t为微带线导体带的厚度，h为基片厚度，W是导体宽度。当w/h≥0.2和2≤ε_r≤50时，计算误差小于4%。

由等效关系：

带入公式：

得到：

也可以使用另一种公式表示：

式中，h为介质基片的厚度；W为导带的宽度；ε_eff为等效相对介电常数；c为真空中的光速。

2）微带线的串联间隙：

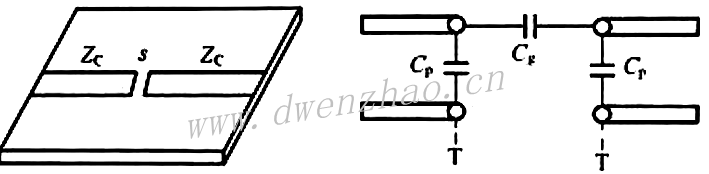
微带线在中间间断而形成一个间隙，这在微带线中也是常见的一种不连续性。在间隙宽度S不大时，间隙可以看成是两条微带线之间的一个串联电容C，也就是说间隙S等效成一个电容C。但微带线的间隙两边的截断处与接地板之间也将各自形成一个并联电容，这样微带线的间隙的等效电路成为一个Π型电容网络，，其等效电路为：

式中，B_a为耦合电容C_g的电抗；B_b为并联电容C_p的电抗；λ_g为微带线中的相波长。当间隙s很小时，可以忽略两个并联电容C_p而只考虑耦合电容C_g。
如果微带线宽度W，间隙S，也可以通过下式计算间隙的电容：

而其中的参数：

有些资料给出下面的计算公式：

式中参数：

式中，C_e/W和C_o/W的单位为pF/m。

3）微带线的对称阶梯：

两条宽度不同，因而特性阻抗不同的微带线连接就会形成微带线的阶梯不连续性，在一般情况下，阶梯大小是对称的，这种不连续性在微带阶梯阻抗变换器和某些滤波器中经常遇到。当导带宽度变小时，线电流密度增加，即磁能增加，这等效于串联电抗呈感抗性质：

式中，Z_C1和Z_C2分别为微带线导体带宽度为W₁和W₂时的特性阻抗，ε_re1和ε_re2则为对应的等效介电常数。

不连续会激励高次模，其作用可用电感和电容元件来等效。另一种等效电路：

其中等效电容计算公式：

下面为等效电感的计算方法，公式中有两种介电常数，可用于不同介质基片的情况。

4）微带线的开槽：

微带线的开槽可用来对电路进行微调。在槽口处串联的电感为：

式中，ε'_r和Z'_C分别为宽度（w-b）的微带线的有效介电常数和特性阻抗。

5）微带线的弯折：

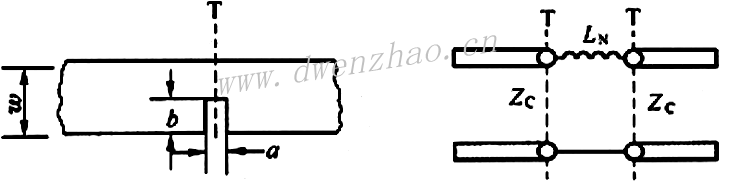
为了改变电磁波传输方向，必须将微带线的导带弯折。一些微带元件在设计上必须要有折弯，如定向耦合器、一些滤波器和功率分配器；为了使微带电路的安排尽可能合理紧凑，也常需要将微带线折弯。 在微带线导体带的各种折弯方式中，使用得最多的是直角折弯，为了尽可能减小由折弯引起的反射，常常将导体带折弯处的顶角切去，成为切角折弯，一般把拐角外边切成45°斜角，其目的就是为了减小拐角处的分布电容。 对于等宽微带拐角，拐角斜边的长度一般约等于1.6倍导带宽度，如左图；如果两边微带线尺寸不等，可按右图所示的尺寸进行设计。图中x₁=0.565W₁，x₂=0.565W₂。也可以使用圆折弯，这时应使导体带中心曲率半径r>3W。

如果为直角拐角，可以等效为右面的LC电路，参数计算公式为：

对于切角的微带线折弯，等效电路中的电感、电容可如下确定：

式中参数：

式中，Z_C,b为导体带宽度为b时微带线的特性阻抗；Z_C,a为当微带线导体带宽度为(W+W_b)/2时微带线的特性阻抗；ε_e(b)为导体宽度为b时的等效介电常数，c为自由空间的光速。

6）微带线的T形接头：

微带线的T形接头在微带电路中具有广泛应用，如并联短截线调配器、分支滤波器和分支电桥中经常用到T形接头。其等效电路中电容的计算公式为：

等效电路中电感的计算公式为：

其中，L₂与分支长度有关；L_Wi是以W_i为宽度的单位长度微带电感。

微带线的T形接头的结构及等效电路见下面左图：

7）微带线的十字接头：

微带线的十字接头在微带电路中也很常用，其结构及等效电路见上右图。等效电路中电容的计算公式为：

等效电路中电感的计算公式为：

8）高低阻抗传输线：

长度为l的传输线终接一负载阻抗Z_L，则传输线输入端阻抗为：

当l<<λ且Z_L<<Z_C（高特性阻抗）时，近似为：

即，高特性阻抗的传输线段近似等效为一串联电感。

当l<<λ且Z_L>>Z_C（低特性阻抗）时，近似为：

即，低特性阻抗的传输线段近似等效为一并联电容。

9）短路短截线：

终端短路线，当l≤λ_g/4时，等效为一并联电感：

10）开路短截线：

终端开路线，当l≤λ_g/4时，等效为一并联电容：

4. 微带线构成的电容和电感：

利用微带传输线在不连续时产生的分布电感和电容，可以作为电路元件来使用。在高频及微波应用时，有时不便使用集总参数的电容和电感，但电路性能上又需要这种元器件，就可以使用这种微带线构成的电路元件来实现特定功能。

1）并联电感和并联电容的实现：

长度为l的终端短路线的输入阻抗为：

当l<λ/4时为感性，当λ/4<l<λ/2时为容性，其电抗与频率的关系是非线性的。
但当l<<λ时，可以近似为：

此时，传输线的输入阻抗就与频率近似呈线性关系了。由此可见，一段终端短路的传输线段，当满足l<<λ时可近似等效为一个集中参数的电感，一般取λ/8~λ/10。

同理，一段长度为l的终端开路线的输入阻抗为：

当满足l<<λ时，可以近似为一个集中参数的电容。

2）串联电感和并联电容的实现：

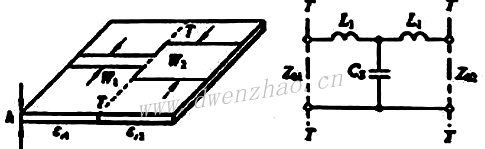
一段长为l特性阻抗为Z_C的传输线可等效为T型电路或Π型电路，等效关系为：

T型电路参数：

Π型电路参数：

可见，无论是T型电路还是Π型电路，其串联元件均为电感，并联元件均为电容。

当l<<λ时，电路中的电抗和电纳可近似为：
T型电路：

Π型电路：

此时等效电路中的电抗和电纳均与频率近似呈线性关系，与集中参数元件的电抗和电纳具有类似的特性。

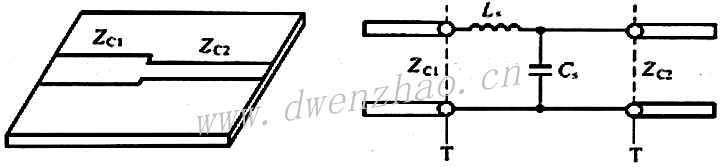
3）高低阻抗线等效电路：

如果传输线段是高阻抗线段，其特性阻抗远大于邻接传输线的特性阻抗，则T型电路中的并联支路可以略去不计，等效电路中只剩下串联电感；如果传输线段是低阻抗线段，其特性阻抗远小于邻接传输线的特性阻抗时，T型电路中的串联支路阻抗可以略去不计，等效电路中只剩下并联电容。
可见，特性阻抗不相同的传输线段串接时，由于特性阻抗之间的相对关系，高阻抗线段可近似等效为串联电感，低阻抗线段可近似等效为并联电容。由于微带线导体带条较窄时阻抗较大，导体带条较宽时特性阻抗较小，所以图中高阻抗微带线和低阻抗微带线可分别等效为串联电感和并联电容，这一特性可用于设计微带低通滤波器。

等效电感和等效电容的计算公式为：

实际中，为了获得较大的电感，可将上述直线电感弯成环形，由于环内磁场相对集中，磁通量增大，所以电感量增大了。如需要进一步增大电感量，还可以做成“蚊香形”平面螺旋电感。

4）串联电容的实现：

微带串联电容通常是用微带间隙来实现，如上面右图所示。微带间隙是将微带导体带条切断所形成的间隙，可看成是两导体带条端面间的串联耦合电容，若再考虑导体带条端面与接地板之间的并联电容，则等效电路是Π型电容网络。 显然，间隙越小，耦合电容越大，而并联电容越小，在间隙很小时等效为一串联电容，而忽略并联电容。
由于导体带条的厚度很小，而宽度也不可能太大，所以导体带条截断端面的面积很小，因此这种电容的电容量不可能做得太大。为了获得大的串联电容，可将导体带条切断处做成“对插形”，这样可以增大截断端面的面积，从而增大串联电容。