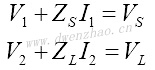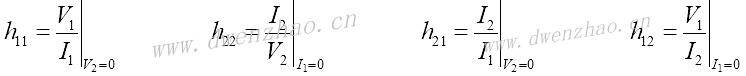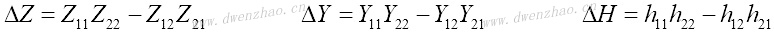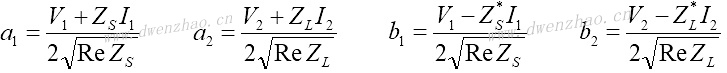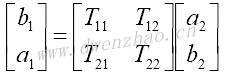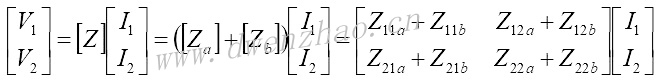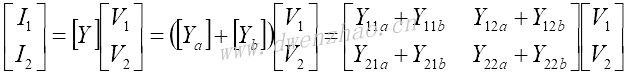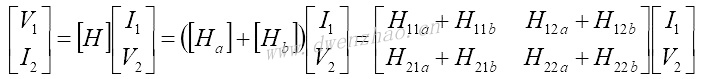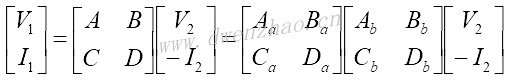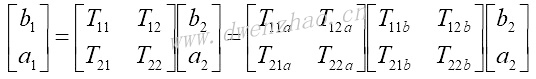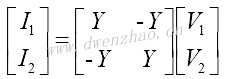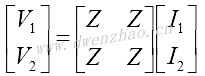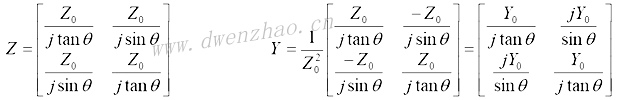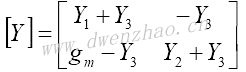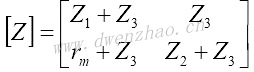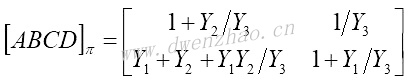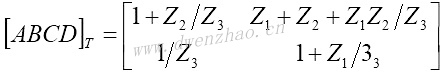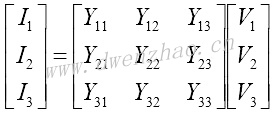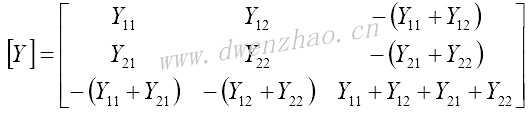赵工的个人空间

二端口网络及参数转换

只具有两个外接端口的电路称为二端口网络，这是电路分析中的常用分析方法。这种方法也可以扩展用来分析射频和微波电路，用于描述有源与无源器件的电性能。先介绍传统的网络参数，然后再介绍扩展到射频微波频段的的散射S参数等。

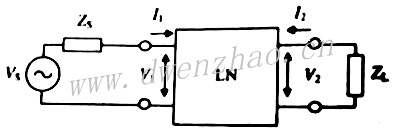
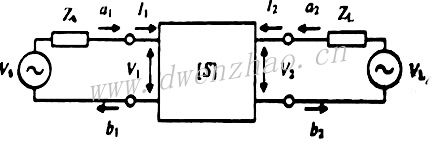
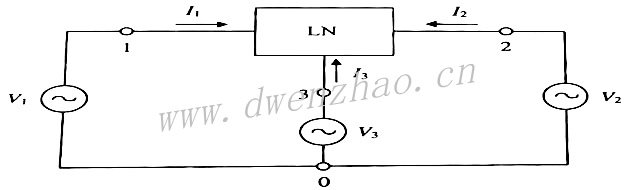
1. 传统网络参数：

一个双口传输系统，基本框图见上图，V_s是独立电压源，Z_s是源阻抗，LN是不具独立源的线性时不变网络，Z_L为负载阻抗。两个独立向量电流I₁和I₂和向量电压V₁和V₂表征这样一个二端口网络。对于自治振荡系统，为提供二端口网络频域的负极性单口网络描述合适的分析，只要设置源阻抗为无穷大即可。

对于上述二端口网络，可以使用多种网络参数来描述，常用的有阻抗参数、导纳参数、混合参数、传输参数等。

1）阻抗Z参数：

对于二端口网络，下式认为叠加了边界条件：

假定所示线性时不变网络可得到唯一解，可转化为开路阻抗二端口网络形式：

其中，Z₁₁和Z₂₂是开路驱动点阻抗；Z₁₂和Z₂₁是二端口网络的开路转移阻抗。驱动点阻抗：

转移阻抗：

2）导纳Y参数：

当电流分量被认为是由电压引起的输出，也可以推导出短路导纳方程：

其中，Y₁₁和Y₂₂是短路驱动点导纳；Y₁₂和Y₂₁是二端口网络的短路转移导纳。驱动点导纳：

转移导纳：

3）混合H参数：

二端口网络可根据输入电流I₁和输出电压V₂来表达电压源V₁和输出电流I₂：

式中的h₁₁、h₁₂、h₂₁、h₂₂是混合H参数。

h₁₁是驱动点输入阻抗，h₂₂是驱动点导纳，h₂₁是正向电流传输函数，h₁₂是反向电压传输函数。

4）传输ABCD参数：

传输参数常用于无源器件分析，可以把网络方程转化为前向传输二端口网络方程形式：

式中的A、B、C、D是传输参数。式中I₂有负号，因为对传输网络来说，输入信号认为是加在输入口的，而输出电流是流向负载，所以-I₂才是进入负载的电流，与上面网络中所画的电流方向相反。

A为反向电压传输函数，B为反向转移阻抗，C为反向转移导纳，D为反相电流传输函数。国内一些相关资料中，经常使用A参数表示传输参数，以上四个参数则分别表示为A₁、A₂、A₃、A₄。

2.传统二端口网络参数之间的转换：

用不同的双口矩阵描述相同的二端口网络，参数之间可以交叉转换，每个矩阵元素可用其他矩阵元素表达，列表为：

	[Z]	[Y]	[H]	[ABCD]
[Z]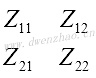
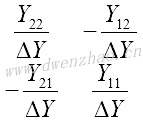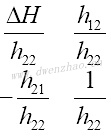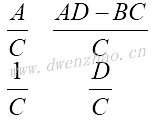[Y]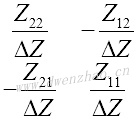
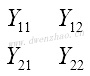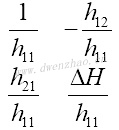[H]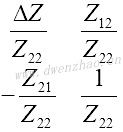
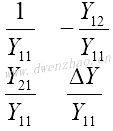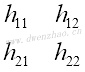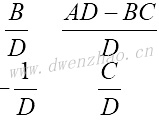[ABCD]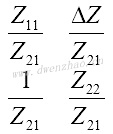

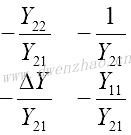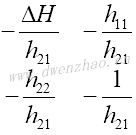3.散射S参数：

在微波系统中，由于确定和测量电压、电流非常困难，代之以测量入射、反射及传输波，建立在入射波、反射波关系基础上的网络参数就是散射参数。散射参数可以直接用网络分析仪测量得到，而网络散射矩阵反映了端口的入射电压波和反射电压波的关系。

归一化反射波b₁和b₂可以用归一化入射波a₁和a₂表示：

对复数源阻抗Z_s和负载阻抗Z_L给定情况下，入射波a₁、a₂和反射波b₁、b₂为：

S₁₁和S₂₁是输出口理想匹配情况下的输入口反射系数及传输系数：

S₁₂和S₂₂是输入口理想匹配情况下的输出口反射系数及传输系数：

还有一种传输散射T矩阵：

T矩阵与S矩阵之间的关系：

4.S参数与Z、Y、H、ABCD参数之间的转换：

Z、Y、H、ABCD参数转换为S参数	S参数转换为Z、Y、H、ABCD参数

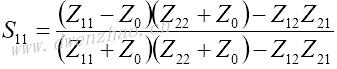
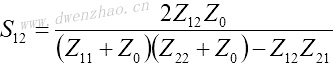
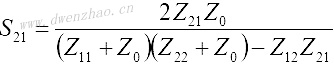
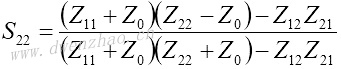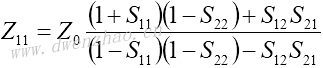
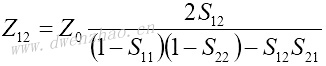
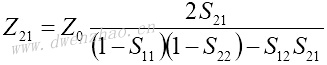
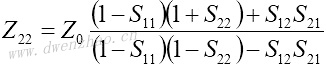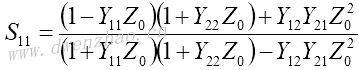
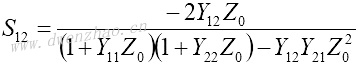
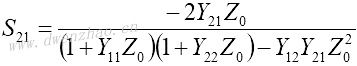
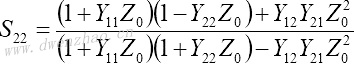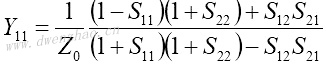
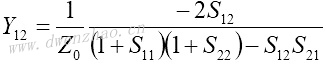
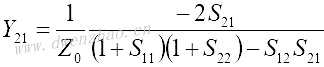
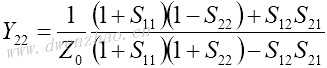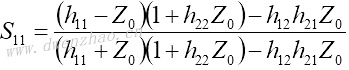
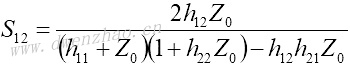
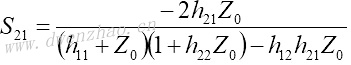
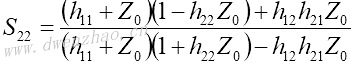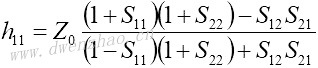
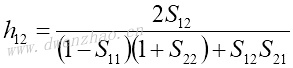
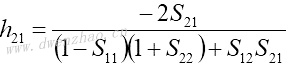
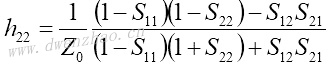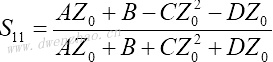
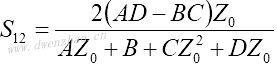
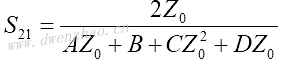
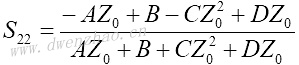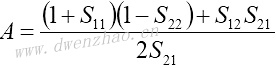
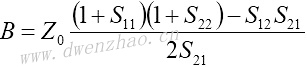
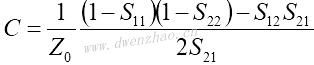
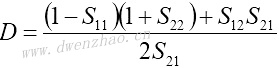5.二端口网络互相连接：：

电路分析时，常需要定义两个或多个内部二端口网络组合后的参数，一般情况下二端口网络间的互相连接可用并联、串联、串并联或级联。

1）网络串联：

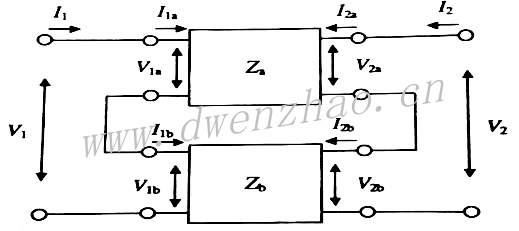
上图所示的二端口网络Z_a和Z_b在输入口和输出口都是串联的，因此流过这些端口的电流是相等的，合成的二端口网络端电压是每个网络端口端电压的简单相加，这种情况下最好使用阻抗矩阵：

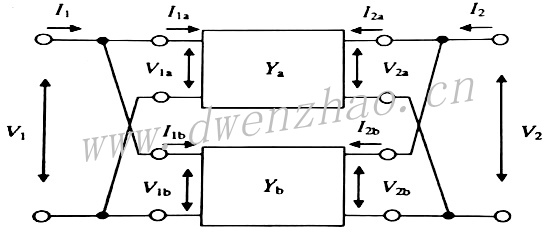
2）网络并联：

上图所示的二端口网络是Y_a和Y_b并联组成，共同分量分别是每个网络的输入和输出电压，这种形式的电路用导纳矩阵来描述更方便：

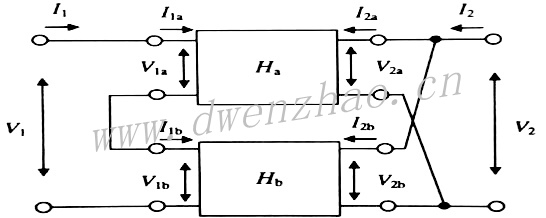
3）网络串并联：

上图是输入口串联而输出口并联的串并联二端口网络，网络共用分量是输入口的电流和输出口的电压，分析这种电路使用混合矩阵最方便：

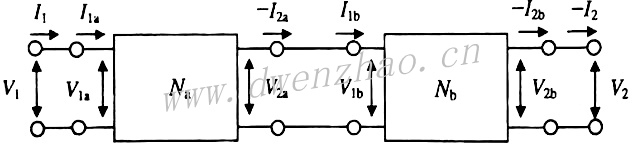
4）网络级联：

上图是两个二端口网络的级联，对这种两个二端口网络一个接一个连接的方式，第一个网络的输出口电流和电压分别等于下一个二端口网络输入口的电流和电压，此时使用ABCD参数最方便：

对于二端口网络的级联，也可以使用T矩阵，等于各个二端口网络T矩阵的乘积。

6.一些常见的二端口网络：

1）单元件网络：

最简单的网络仅包含一个元件，可构成串联导纳Y或并联阻抗Z，如图：

由串联导纳Y构成的二端口网络可以写成矩形形式：

其中Y矩阵是奇异矩阵，|Y|=0，这种二端口网络不能用Z参数来表示，都可以使用H和ABCD参数表示：

而并联阻抗网络可以表示为：

其中的Z矩阵也是奇异矩阵，|Z|=0，这种二端口网络不能用Y参数表示，但也可以使用H和ABCD参数表示：

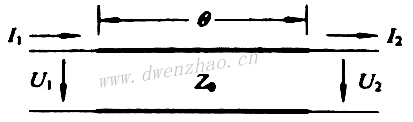
2）一段传输线网络：

一段特性阻抗为Z₀的传输线也是一个二端口网络，如图：

其阻抗参数及导纳参数矩阵为：

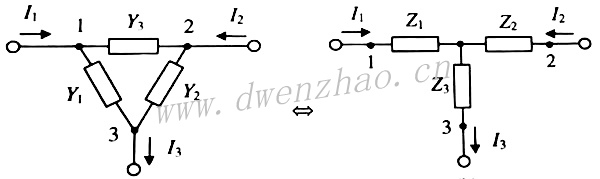
3）π形和T形网络：

上面左图是π形网络，其中包含电流源g_mV₁；右图为T形网络，其中包含电压源r_mI₁。π形网络用Y参数表示为：

T形网络用Z参数表示为：

当π形网络中的g_m=0和T形网络的r_m=0时，ABCD参数可以分别表示为：

为找到T形阻抗参数和π形导纳参数之间的关系，将电路画成上图的形式。可以从中解出电压和电流，然后得到π形电路与T形电路等效时的参数关系：

T到π形的变换	π到T形的变换

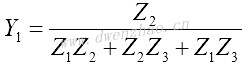
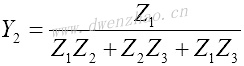
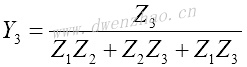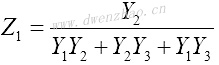
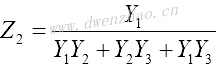
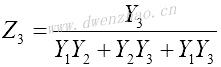4）具有公共端口的三口网络：

当三个独立源全部接到公共端口时，具有两个独立源的二端口网络概念能扩展成多口，如下图。

将上述网络可以写为导纳矩阵：

式中的Y矩阵为三口导纳矩阵，是一个奇异矩阵，因为进入电路的端电流总和为零，所有进入电路的端电流依赖于电路端之间的电压，因此使所有端电压的总和为零。由此：

应用以上结果，可以得到三口网络的导纳矩阵：

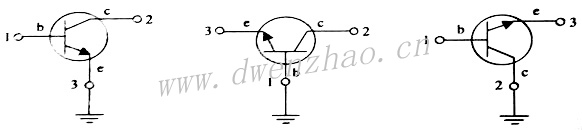
依次选择1、2、3作为公共端口，能得到适宜的三个确定的最初为三口网络的二端口导纳矩阵，这些二端口导纳矩阵分别是下图所示的双极晶体管的共射、共基、共集组态。

如果共射器件视为由四个参数Y₁₁、Y₁₂、Y₂₁、Y₂₂描述特征的二端口电路，则集电极接地的二端口共集电路矩阵则简单地从Y矩阵中划掉第二行和第二列即可；基极接地的共基组态，则需要划掉第一列和第一行，因为此时发射极是作为输入端。

类似的方法能应用于不定三口阻抗矩阵，从已知的共射组态阻抗矩阵Z参数，可得到共基和共集阻抗矩阵的Z参数。双极晶体管和场效应管，三口网络不同公共端口的参数：

	Y参数	Z参数
共射/共源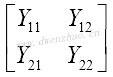
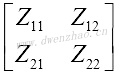共基/共栅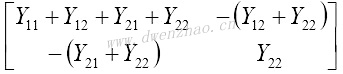
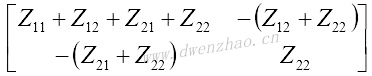共集/共漏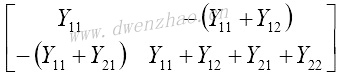

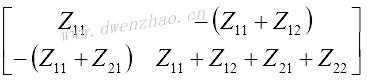5）二端口网络输入反射系数与负载反射系数的关系：

对一个S参数已知的二端口网络，如果测得输出口的负载反射系数为Γ_L，则可以得到输入口的反射系数Γ_in：

而已知负载阻抗或导纳时二端口网络的输入阻抗和导纳为：