赵工的个人空间

神经网络工具箱是在MATLAB环境下开发出的许多工具箱之一，它以人工神经网络理论为基础，利用MATLAB编程语言构造出许多典型的神经网络框架和相关函数。其中的工具函数主要分为两大部分，一部分是特别针对某一种类型的神经网络的，如感知器创建函数、BP网络的训练函数等；另一部分是通用的，几乎可以用于所有类型的神经网络，如神经网络仿真函数、初始化函数和训练函数等。

1. 神经网络工具箱中的通用函数：

通用函数见表：

1）神经网络仿真函数sim：用于对神经网络进行仿真
[Y,Pf,Af,E,perf]=sim(net,P,Pi,Ai,T)
[Y,Pf,Af,E,perf]=sim(net,{Q TS},Pi,Ai,T) %常用于没有输入信号的回归神经网络
[Y,Pf,Af,E,perf]=sim(net,Q,Pi,Ai,T)
其中，Y为网络输出；Pf为最终输出延迟；Af为最终的层延迟；E为网络误差；perf为网络性能。net为待仿真的神经网络；P为网络输入；Pi为初始输入延迟，默认为0；Ai为初始的层延迟，默认为0；T为网络目标，默认为0。Pi、Ai、Pf和Af是可选的，只用于存在输入延迟和层延迟的网络。
函数中的信号参数采用单元阵列和矩阵的形式，其中单元阵列能够方便地对多输入多输出的神经网络进行描述，其中的阵列或矩阵形式为：
·P：NixTS维单元阵列，每个元素P{i,ts}都是一个RixQ的矩阵
·Pi：NixID维单元阵列，每个元素Pi{i,k}都是一个RixQ的矩阵
·Ai：NlxLDS维单元阵列，每个元素Ai{i,k}都是一个SixQ的矩阵
·T：NtxTS维单元阵列，每个元素T{i,ts}都是一个VixQ的矩阵
·Y：NoxTS维单元阵列，每个元素Y{i,ts}都是一个UixQ的矩阵
·Pf：NixID维单元阵列，每个元素Pf{i,k}都是一个RixQ的矩阵
·Af：NlxLD维单元阵列，每个元素Af{i,k}都是一个SixQ的矩阵
·E：NtxTS维单元阵列，每个元素E{i,ts}都是一个VixQ的矩阵
其中，Ni为神经网络输入的数目；Nl为神经网络层次的数目；No为神经网络输出的数目；ID为输入延迟的数目；LD为层次延迟的数目；TS为时间步长的数目；Q为批量；Ri为第i个输入的长度；Si为第i层的长度；Ui的第i个输出的长度；Pi{i,k}为第i个输入在ts=k-ID时刻的状态；Pf{i,k}为第i个输入在ts=TS+k-ID时刻的状态；Ai{i,k}为某层输出i在ts=k-LD时刻的状态；Af{i,k}为某层输出i在ts=TS+k-LD时刻的状态。
矩阵的形式只用于仿真的时间步长TS=1的场合，每个矩阵都是由对应的单元阵列中的元素组合而成：
·P：Ri的总和XQ维矩阵
·Pi：Ri的总和X(ID*Q)维矩阵
·Ai：Ri的总和X(LD*Q)维矩阵
·T：Ri的总和XQ维矩阵
·Y：Ri的总和XQ维矩阵
·Pf：Ri的总和X(ID*Q)维矩阵
·Af：Ri的总和X(LD*Q)维矩阵
·E：Ri的总和XQ维矩阵
2）神经网络训练和学习函数：
⑴train：用于对神经网络进行训练
[net,tr,Y,E,Pf,Af]=train(NET,P,T,Pi,Ai)
[net,tr,Y,E,Pf,Af]=train(NET,P,T,Pi,Ai,VV,TV)
其中，NET为待训练神经网络；P为网络的输入信号；T为网络的目标，默认0；Pi为初始的输入延迟，默认0；VV为网络结构确认向量，默认空；TV为网络结构测试向量，默认空；net为训练后的神经网络；tr为训练记录；Y为神经网络输出信号；E为神经网络误差；Pf为最终输入延迟；Af为最终层延迟。
其中T是可选的，只有当需要明确神经网络的目标时才调用；Pi和Pf也可选，只用于存在输入延迟和层延迟的场合；VV和TV也可选，除了采用空矩阵外，只能从以下范围取值：
·VV.P/TV.P：确认/测试输入信号；
·VV.T/TV.T：确认/测试目标，默认0；
·VV.Pi/TV.Pi：确认/测试初始的输入延迟，默认0；
·VV.Ai/TV.Ai：确认/测试层确认延迟，默认为0。
调用该函数对网络进行训练之前，需要先设定实际的训练函数，如trainlm或traingdx等，然后该函数调用相应的算法对网络进行训练。
⑵trainb：用于神经网络权值和阈值的训练
[NET,TR,Ac,El]trainb(net,Pd,Tl,Ai,Q,TS,VV,TV)
info=trainb(code)
其中，net为待训练的神经网络；Pd为已延迟的输入信号；Tl为层目标；Ai为初始的输入；Q为批量；TS为时间步长；VV为确认向量或者空矩阵；TV为测试向量或者空矩阵；NET为训练后的神经网络；TR为每一步的训练记录，包括仿真步长TR.epoch，训练性能TR.pert，确认性能TR.vpert，测试性能TR.tperf；Ac为训练停止后聚合层的输出；El为训练停止后的层误差。
训练之前需要设定以下参数：

该函数并不能直接调用，而是通过train函数隐含调用，通过设置网络属性NET.trainFcn为trainb来调用trainb对网络进行训练。
⑶learnp：用于神经网络权值和阈值的学习
[dW,LS]=learnp(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
[dW,LS]=learnp(b,ones(1,Q),Z,N,A,T,E,gW,gA,D,LP,LS)
info=learnp(code)
其中，W为SxR维的权值矩阵，或Sx1维的阈值向量；P为Q组R维的输入向量，或Q组单个输入；Z为Q组S维的权值输入向量；N为Q组S维的网络输入向量；A为Q组S维的输出向量；T为Q组S维的目标向量；E为Q组S维的误差向量；gW为SxR维的性能参数的梯度；gA为Q组S维的性能参数的输出梯度；LP为学习参数，若没有则为空；LS为学习状态，初始值为空；dW为SxR维权值或阈值的变化矩阵；LS为新的学习状态。
info=learnp(code)对不同的code返回相应的有用信息，包括pnames返回学习参数的名称，pdefaults返回默认的学习参数，needg如果函数使用了gW或gA时返回1。
⑷learnpn：权值和阈值学习函数
在输入向量的幅值变化非常大或者存在奇异值时，其学习速度比learnp要快得多。
[dW,LS]=learnpn(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
info=learnpn(code)
⑸adapt：使得神经网络能够自适应
[net,Y,E,Pf,Af,tr]=adapt(NET,P,T,Pi,Ai)
其中，NET为自适应的神经网络；P为网络输入；T为网络目标，默认0；Pi为初始输入延迟，默认0；初始层延迟，默认0。
通过设定自适应的参数net.adaptParam和自适应的函数net.adaptFunc可调用该函数，并返回参数：net为自适应后的神经网络；Y为网络输出；E为网络误差；Pf为最终输入延迟；Af为最终层延迟；tr为训练记录，步数和性能。
参数T是可选的，并且只用于必须指明网络目标的场合；Pi和Pf可选，只用于存在输入延迟和层延迟的网络。
⑹revert：用于将更新后的权值和阈值恢复到最后一次初始化的值
net=revert(net)
如果网络结构已经发生了变化，那么该函数无法将权值和阈值恢复到原来的值，这种情况下函数将权值和阈值都设置为0。
3）神经网络初始化函数：
⑴init：用于对神经网络进行初始化
NET=init(net)
其中，NET表示已经初始化后的神经网络；net为待初始化的神经网络。
⑵initlay：适用于层-层结构的神经网络的初始化
NET=inilayt(net)
info=inilayt(code)
其中，net为待初始化的神经网络；NET为初始化后的神经网络。
info=inilayt(code)根据不同的code码返回不同的信息，包括初始化参数名称pnames，默认的初始化参数pdefault。
通过指定神经网络每一层i的初始化函数NET.layers{i}来调用该函数，初始化后的神经网络每一层都得到了修正。
⑶initnw：层初始化函数
按照Nguyen-Widrow准则对某层的权值和阈值进行初始化
NET=initnw(net,i)
其中，net为待初始化的神经网络；i为层次索引；NET为初始化后的神经网络
⑷initwb：层初始化函数
按照设定的每层的初始化函数对每层的权值和阈值进行初始化
NET=initwb(net,i)
其中，net为待初始化的神经网络；i为层次索引；NET为初始化后的神经网络
4）神经网络输入函数：
⑴netsum：输入求和函数
通过将某一层的加权输入和阈值相加作为该层的输入。
N=netsum(Z1,Z2,...)
df=netsum('deriv') %返回netsum的微分函数
其中，Zi为第i个输入，数目可以是任意个。
⑵netprod：输入求积函数
将某一层的权值和阈值相乘作为该层的输入。
N=netprod(Z1,Z2,...)
df=netprod('deriv') %返回netprod的微分函数
其中，Zi为第i个输入，数目可以是任意个。
⑶concur：使得本来不一致的权值向量和阈值向量的结构一致，以便相加或相乘运算
concur(b,q)
其中，b为Nlx1维权值向量；q为要达到一致化所需要的长度。返回值是经一致化的矩阵。
5）神经网络传递函数：
传递函数的作用是将神经网络的输入转换为输出。
⑴hardlim：硬限幅传递函数
A=hardlim(N)
info=hardlim(code)
其中，N为某层的Q组S维的输入向量；A返回该层的输出向量，当N>0时返回值为1，当N<0时返回值为0。
info=hardlim(code)根据不同的代码code返回不同的信息，包括导数函数名称deriv、传递函数全称name、传递函数输出范围output、传递函数输入范围active。
可通过将NET.layers{i}.transferFcn设定为hardlim来调用该函数，这设置了神经网络中第i层的传递函数。该函数原型是：

⑵hardlims：对称的硬限幅传递函数
A=hardlims(N)
info=hardlims(code)
其中，N为某层的Q组S维的输入向量；A返回该层的输出向量，当N>0时返回值为1，当N<0时返回值为-1。该函数原型是：

6）其他重要函数：
dotprod：用于对权值求点积，求得权值与输入之间的点积作为加权输入
Z=dotprod(W,P)
df=dotprod('deriv') %返回函数的导数
其中，W为SxR维的权值矩阵；P为Q组R维的输入向量；Z为Q组R维的W与P的点积

2. 感知器的神经网络工具箱函数：

感知器网络是罗森布拉特于1957年提出，可以说是最早的人工神经网络。单层感知器是一个具有单层神经元、采用阈值激活函数的前向网络。通过对网络权值的训练，可以使感知器对一组输入矢量的响应达到元素为0或1的目标输出，从而实现对输入矢量进行分类的目的。
常用的感知器函数为：

1）感知器创建函数：
net=newp %打开一个对话框来定义感知器的属性
net=newp(pr,s,tf,lf)
其中，net为生成的感知器网络；pr为Rx2矩阵，由R组输入向量的最大值和最小值组成；s为神经元的个数；tf为感知器的传递函数，可选参数为hardlim和hardlims，默认为hardlim；lf为感知器的学习函数，可选参数为learnp和learnpn，默认为learnp。
2）显示函数：
⑴plotpc：用于在感知器向量图中绘制分界线
plotpc(W,b) %返回对所绘制分界线的控制器
plotpc(W,b,h) %用于在绘制新线之前检查最新绘制的分界线
其中，W为SxR维的加权矩阵，R必须小于等于3；b为Sx1维的阈值向量；h为最后画线的控制权。
该函数一般在plotpv函数之后调用，并不改变现有的坐标轴标准
⑵plotpv：用于绘制感知器的输入向量和目标向量
plotpv(p,t) %以t为标尺绘制p的列向量
plotpv(p,t,v) %在v的范围中绘制p的列向量
其中，p为Q组R维的输入向量；t为Q组S维的双目标向量；v=[x_min x_max y_min y_max]为图像的最大值，绘制必须位于v所限定的范围中。
3）性能函数：
mae函数是以平均绝对误差为准则，确定神经网络性能的函数。
perf=mae(e,x,pp)
perf=mae(e,net,pp)
info=mae(code)
其中，e为误差向量矩阵或误差向量；x为所有的权值和阈值向量，可忽略；pp为性能参数，可忽略；net为待评定的神经网络；perf为平均绝对误差。
info=mae(code)根据code值的不同返回不同的信息，导数函数的名称deriv，函数全名name，训练参数的名称pnames，默认的训练参数pdefaults。
感知器最重要的也是最实用的功能是对输入向量进行分类。

3. 线性网络的神经网络工具箱函数：

线性网络是由Widrow和Hoff于1960年提出的一种网络模型，其结构和感知器类似，属于单层的神经网络，因为训练算法是自适应滤波的LMS算法，所以是一个自适应可调的网络，适用于信号处理中的自适应滤波、预测和模型识别。
线性网络常用函数为：

1）线性网络创建函数：
⑴newlin：创建一个线性层
线性层是一个单独的层次，它的权函数为dotprod，输入函数为netsum，传递函数为purelin。线性层一般用作信号处理和预测中的自适应滤波器。
net=newlin %打开一个对话框来创建一个新的网络
net=newlin(PR,S,ID,LR)
其中，PR是由R个输入元素的最大值和最小值组成的Rx2维矩阵；S为输出向量的数目；ID为输入延迟向量，默认为[0]；LR为学习速率，默认0.01；net为返回值，是一个新的线性层。
如果0替代参数ID，用输入向量矩阵P替代参数LR，那么函数返回的线性层的稳定学习速率对于P来说是最大的。
⑵newlind：设计一个线性层，它通过输入向量和目标向量来计算线性层的权值和阈值
net=newlind %打开一个对话框来创建一个新的网络
net=newlind(P,T,Pi)
其中，P为Q组输入向量组成的RxQ维矩阵；T为Q组目标分类向量组成的SxQ维矩阵；Pi为初始输入延迟状态的ID个单元矩阵，每个元素Pi{i,k}都是一个RixQ维的矩阵，默认为空；net为函数返回值，是一个线性层，它的输出误差平方和对于输入P来说具有最小值。
2）学习函数：
⑴learnwh：Widrow-Hoff学习函数，也称为delta准则或最小方差准则学习函数
它可以改变神经元的权值和阈值，使输出误差的平方和最小，沿着误差平方和下降最快方向连续调整网络的权值和阈值。由于线性网络的误差性能表面是抛物面，仅有一个最小值，因此可以保证网络是收敛的，前提是学习率不超出maxlinlr计算得到的最大值。
[dW,LS]=learnwh(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
[dW,LS]=learnwh(b,ones(1,Q),Z,N,A,T,E,gW,gA,D,LP,LS)
info=learnwh(code)
其中，W为SxR维的加权矩阵，或为Sx1的阈值矩阵；P为Q个R维的输入向量，或为Q个单值输入；Z为Q组S维的加权输入向量；N为Q组S维的网络输入向量；A为Q组S维的输出向量；T为Q组S维的目标向量；E为Q组S维的误差向量；gW为SxR维的性能参数的梯度；gA为Q组S维的性能参数的输出梯度；LP为学习参数，若没有则为空；LS为学习状态，初始值为空；dW为SxR维权值或阈值的变化矩阵；LS为新的学习状态。
info=learnwh(code)针对不同的code返回相应的有用信息，返回学习参数pnames，返回默认的学习参数pdefaults，如果使用了gW或gA则needg返回1。
函数的学习参数LP可以自行设定，如设定学习速率LP.lr=0.01，这是默认值。
⑵maxlinlr：分析函数，用于计算线性层的最大学习速率
lr=maxlinlr(P) %针对不带阈值的线性层得到一个所需要的最大学习速率
lr=maxlinlr(P,'bias') %针对带有阈值的线性层得到一个所需要的最大学习速率
其中，P为输入向量的RxQ维矩阵。一般来说，学习速率越大，所需的训练时间越少；但是如果学习速率过大，容易造成学习过程的不稳定。
由newlin创建的线性网络，权值函数为dotprod，输入函数为netsum，神经元传递函数为purelin，权值和阈值的初始化函数为initzero，学习函数为learnwh，性能函数为mse。

4. BP网络的神经网络工具箱：

BP网络全称是Back-Propagation Network，即反向传播网络。BP网络是一个前向多层网络，它利用误差反向传播算法对网络进行训练，结构简单、可塑性强，在函数逼近、模式识别、信息分类及数据压缩等领域得到了广泛的应用。
BP网络的常用函数有：

1）BP网络创建函数：
⑴newcf：用于创建级联前向BP网络
net=newcf %打开一个对话框来创建一个BP网络
net=newcf(PR,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF)
其中，PR为由每组输入元素的最大值和最小值组成的Rx2维矩阵，共有R组输入；Si为第i层的长度，共计Nl层；TFi为第i层的传递函数，默认tansig；BTF为BP网络的训练函数，默认trainlm；BLF为权值和阈值的BP学习算法，默认learngdm；PF为网络性能函数，默认mse。
参数TFi可以采用任意的可微传递函数，比如tansig、logsig和purelin等；训练函数可以是任意的BP训练函数，如trainlm、trainbfg、trainrp和traingd等。BTF默认采用trainlm，因为该函数速度很快，但运行过程会消耗大量内存资源，如果内存不够大，建议采用trainbfg或trainrp，这两种函数运行较慢，但内存占用小。
⑵newff：用于创建一个BP网络
net=newff %打开一个对话框来创建一个BP网络
net=newff(PR,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF)
其中参数见newcf函数说明。
⑶newfftd：用于创建一个存在输入延迟的前向网络
net=newfftd %打开一个对话框来创建一个BP网络
net=newfftd(PR,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF)
2）神经元上的传递函数：
传递函数是BP网络的重要组成部分。传递函数又称为激活函数，必须是连续可微的。BP网络经常采用S型的对数或正切函数和线性函数。
⑴logsig：S型的对数函数
A=logsig(N)
info=logsig(code)
其中，N为Q个S维的输入列向量；函数返回值A位于区间(0,1)中。
info=logsig(code)依据code值的不同返回不同的信息，返回微分函数名称deriv，返回函数全称name，返回输出值域output，返回有效的输入区间active。
MATLAB使用的对数传递函数的公式为：

⑵dlogsig：为logsig的导函数
dA_dN=dlogsig(N,A)
其中，N为SxQ维网络输入；A为SxQ维网络输出；函数返回值dA_dN为输出对输入的导数。MATLAB使用的对数传递函数的导数公式为：y=x*(1-x)。
⑶tansig：为双曲正切S型函数
A=tansig(N) %依据code值的不同返回不同的信息，说明同logsig
info=tansig(code)
其中，N为Q个S维的输入列向量；函数返回值A位于区间(-1,1)之间。
MATLAB使用的双曲正切传递函数的公式为：

⑷dtansig：为tansig的导函数
dA_dN=dtansig(N,A)
其中，N为SxQ维网络输入；A为SxQ维网络输出；函数返回值dA_dN为输出对输入的导数。MATLAB使用的双曲正切传递函数的导数公式为：y=1-x*x。
⑸purelin：为线性传递函数
A=purelin(N) %依据code值的不同返回不同的信息，说明同logsig
info=purelin(code)
其中，N为Q个S维的输入列向量；函数返回值A=N。MATLAB使用的线性传递函数的公式为y=x。
⑹dpurelin：为purelin的导函数
dA_dN=dpurelin(N,A)
MATLAB使用的线性传递函数的导数公式为常数函数：y=1。
3）BP网络学习函数：
⑴learngd：梯度下降权值/阈值学习函数
通过神经元的输入和误差，以及权值和阈值的学习速率，来计算权值和阈值的变化率。
[dW,ls]=learngd(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
[db,ls]=learngd(b,ones(1,Q),Z,N,A,T,E,gW,gA,D,LP,LS)
info=learngd(code)
其中，W为SxR维的权值矩阵；b为S维的阈值向量；P为Q组R维的输入向量；ones(1,Q)产生一个Q维的输入向量；Z为Q组S维的加权输入向量；N为Q组S维的输入向量；A为Q组S维的输出向量；T为Q组S维的层目标向量；E为Q组S维的层误差向量；gW为与性能相关的SxR维梯度；gA为与性能相关的SxR维输出梯度；D为SxS维的神经元距离矩阵；LP为学习参数，可通过该参数设置学习速率，设置格式如LP.lr=0.01；LS为学习状态，初始状态下为空；dW为SxR维的权值或阈值变化率矩阵；db为S维的阈值变化率向量；ls为新的学习状态。
info=learngd(code)根据不同的code值返回有关函数的不同信息，返回设置的学习参数pnames、返回默认的学习参数pdefaults、如果函数使用了gW或gA参数needg返回1。
⑵learngdm：梯度下降动量学习函数
它利用神经元的输入和误差、权值或阈值的学习速率和动量参数，来计算权值或阈值的变化率。
[dW,ls]=learngdm(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
[db,ls]=learngdm(b,ones(1,Q),Z,N,A,T,E,gW,gA,D,LP,LS)
info=learngdm(code)
动量参数mc是通过学习参数LP设置的，格式为lp.mc=0.8。
4）BP网络训练函数：
⑴trainbfg：为BFGS准牛顿BP算法函数
[net,TR,Ac,El]=trainbfg(NET,Pd,Tl,Ai,Q,TS,VV,TV)
info=trainbfg(code)
其中，NET为待训练的神经网络；Pd为有延迟的输入向量；Tl为层次目标向量；Ai为初始的输入延迟条件；Q为批量；TS为时间步长；VV为确认向量结构或者为空；TV为检验后的神经网络；net为训练后的神经网络；TR为每步训练的有关信息记录，包括时间点TR.epoch、训练性能TR.perf、确认性能TR.vperf、检验性能TR.tperf；Ac为上一步训练中聚合层的输出；El为上一步训练中的层次误差。
info=trainbfg(code)根据不同的code值返回不同的有关trainbfg的信息，返回设定的训练参数pnames，返回默认的训练参数pdefaults。
MATLAB默认以下训练参数：

该函数也可以训练任意形式的神经网络，只要它的传递函数对于权值和输入存在导函数。
⑵traingd：为梯度下降BP算法函数
[net,tr,Ac,El]=traingd(net,Pd,Tl,Ai,Q,Ts,VV,TV)
info=traingd(code)
参数、格式与适用范围见trainbfg函数说明。
⑶traingdm：为梯度下降动量BP算法函数
[net,tr,Ac,El]=traingdm(net,Pd,Tl,Ai,Q,Ts,VV,TV)
info=traingdm(code)
参数、格式与适用范围见trainbfg函数说明。
MATLAB神经网络工具箱还有一系列可用于BP网络训练的训练函数：

以上的训练函数，不仅可用于BP网络的训练，还适用于其他任何神经网络，只要其传递函数对于权值和阈值存在导函数即可。
5）性能函数：
⑴mse：为均方误差性能函数
perf=mse(e,x,pp)
perf=mse(e,net,pp)
info=mse(code)
各参数含义见mae函数。
⑵msereg：通过两个因子的加权和来评价网络的性能
两个因子分别是均方误差、均方权值和阈值。
perf=msereg(e,x,pp)
perf=msereg(e,net,pp)
info=msereg(code)
在使用该函数之前，需要设定性能参数pp，格式为PP.radio=0.3，该参数的意义是误差相对于权值和阈值的重要性，函数返回值=均方误差xPP.ratio+均方权值和阈值xPP.ratio。
6）显示函数：
⑴plotperf：用于绘制网络的性能
plotperf(tr,goal,name,epoch)
其中，tr为网络训练记录；goal为性能目标，默认NaN；name为训练函数名，默认为空；epoch为训练步数，默认为训练记录长度。
函数除了可以绘制网络的训练性能外，还可以绘制性能目标、确认性能和检验性能，前提是它们都存在。
⑵plotes：用于绘制一个单独神经元的误差曲面
plotes(wv,bv,es,v)
其中，wv为权值的N维行向量；bv为M维阈值行向量；es为误差向量组成的MxN维矩阵；v为视角，默认为[-37.5,30]。
函数绘制的误差曲面图是由权值和阈值确定的，由函数errsurf计算得出。
⑶plotep：用于绘制权值和阈值在误差曲面上的位置
H=plotep(w,b,e)
H=plotep(w,b,e,h)
其中，w为当前权值；b为当前阈值；e为当前单输入神经元单位误差；h为权值和阈值在上一时刻的位置信息向量；H为当前的权值和阈值位置信息向量。
在整个绘制过程中，H可以看作一个临时存储变量。在绘制新的权值和阈值位置之前H被清除，在绘制后H记录了本次权值和阈值的位置信息。
⑷errsurf：用于计算单个神经元的误差曲面
E=errsurf(P,T,WV,BV,F)
其中，P为输入行向量；T为目标行向量；WV为权值列向量；BV为阈值列向量；F为传递函数名。神经元的误差曲面是由权值和阈值的行向量确定的。
BP网络的一个重要功能是非线性映射，适合于函数逼近等，即找出两组数据之间的关系。利用newff创建的前向型网络，每层的权值函数都为dotprod，输入函数为netsum，层的初始化函数为initnw。

5. 反馈网络的神经网络工具箱函数：

动态神经网络Recurrent Network又称反馈神经网络，其输出不仅和当前网络的输入有关，也和网络以前的输出、输入有关。反馈网络，从反馈形式来看，一种是输入有延迟的时间延迟回馈网络，另一种是输入有延迟，输出有回馈的层回馈网络。
反馈网络常用的工具箱函数为：

反馈网络比较典型的有Hopfield网络和Elman网络，Hopfield应用主要集中于图像和语音串联、数据查询、容错控制、模式分类和识别等。Elman网络属于层反馈，是在BP网络基本结构的基础上，通过存储内部状态使其具备映射动态特征的功能，从而使系统具有适应时变特性的能力。
Hopfield和Elman网络提供了一些工具函数：

1）反馈网络的创建函数：
⑴newfftd：用于设计一个聚焦时间延迟神经网络
聚焦时间延迟神经网络是反馈网络的一种，通常用于系统控制。
net=newfftd %打开一个对话框来创建一个聚焦时间延迟神经网络
net=newfftd(PR,ID,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF)
其中，PR为R组输入元素的最小值和最大值的设定值，Rx2维矩阵；ID为延迟输入向量；Si为第i层的长度；TFi为第i层的传递函数，默认tansig；BTF为BP网络的训练函数，默认为traingdx；BLF为BP网络的权值/阈值学习函数，默认为learngdm；PF为性能函数，默认mse。
参数BTF可以取traingd、traingdm、traingda和traingdx等训练函数；BLF可以取学习函数learngd和learngdm；PF可以取性能函数mse和msereg。
⑵newdtdnn：用于设计一个分布时间延迟神经网络
分布时间延迟网络是反馈网络的一种，通常用于系统控制。
net=newdtdnn %打开一个对话框来创建一个分布时间延迟神经网络
net=newdtdnn(PR,[D1 D2...DNl],[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF)
其中，PR为R组输入元素的最小值和最大值的设定值，Rx2维矩阵；Di为延迟输入向量；Si为第i层的长度；TFi为第i层的传递函数，默认tansig；BTF为BP网络的训练函数，默认为traingdx；BLF为BP网络的权值/阈值学习函数，默认为learngdm；PF为性能函数，默认mse。
参数BTF可以取traingd、traingdm、traingda和traingdx等训练函数；BLF可以取学习函数learngd和learngdm；PF可以取性能函数mse和msereg。
⑶newnarx：用于设计一个平行输入非线性回归神经网络
平行输入非线性回归神经网络是反馈网络的一种，通常用于系统控制。
net=newnarx %打开一个对话框来创建一个平行输入非线性回归神经网络
net=newnarx(PR,ID,OD,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF)
其中，PR为R组输入元素的最小值和最大值的设定值，Rx2维矩阵；ID为延迟输入向量；OD为延迟输出向量；Si为第i层的长度；TFi为第i层的传递函数，默认tansig；BTF为BP网络的训练函数，默认为traingdx；BLF为BP网络的权值/阈值学习函数，默认为learngdm；PF为性能函数，默认mse。
参数BTF可以取traingd、traingdm、traingda和traingdx等训练函数；BLF可以取学习函数learngd和learngdm；PF可以取性能函数mse和msereg。
⑷newnarxsp：用于设计一个串联输入非线性回归神经网络
串联输入非线性回归神经网络是反馈网络的一种，通常用于系统控制。
net=newnarxsp %打开一个对话框来创建一个串联输入非线性回归神经网络
net=newnarxsp({PR1 PR2},ID,OD,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF)
其中，PRi为R组输入元素的最小值和最大值的设定值，Rx2维矩阵；ID为延迟输入向量；OD为延迟输出向量；Si为第i层的长度；TFi为第i层的传递函数，默认tansig；BTF为BP网络的训练函数，默认为traingdx；BLF为BP网络的权值/阈值学习函数，默认为learngdm；PF为性能函数，默认mse。
参数BTF可以取traingd、traingdm、traingda和traingdx等训练函数；BLF可以取学习函数learngd和learngdm；PF可以取性能函数mse和msereg。
⑸sp2narx：用于把串联输入的网络转换为平行输入的非线性回归神经网络
net=sp2narx(net)
其中，net为用来的串联输入非线性回归神经网络。
2）Hopfield的工具箱函数：
⑴newhop：用于设计一个Hopfield网络
net=newhp %打开一个对话框来创建一个Hopfield网络
net=newhop(T)
其中，T为Q个目标向量组成的RxQ维矩阵，矩阵元素必须为1或-1；返回值net为创建的Hopfield网络，稳定点位于目标向量T中。
⑵satlins：为饱和线性传递函数，通常用作Hopfield网络的传递函数
A=satlins(N)
info=satlins(code)
其中，N为输入（列）向量的SxQ维矩阵；返回值A限制在区间[-1 1]中。
info=satlins(code)根据不同的code值返回不同的有关函数的信息，返回导函数deriv，返回函数全称name，返回输出范围output，返回可用输入范围active。函数原型为：

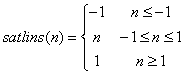
由于Hopfield不存在输入向量，因此当函数sim的第二个参数采用矩阵形式时，Q=2；当采用单元阵列的形式时，{Q TS}=[1 5]。Hopfield网络特别适合于模式回想，回想性能特别适合于图像补正、自动目标识别等领域。
利用newhop创建的Hopfield网络，权值函数采用dotprod，输入函数采用netsum，传递函数采用stalins，而网络的权值是自身的反馈。
3）Elman网络的工具箱函数：
newelm函数用于设计一个Elman网络。
net=newelm %打开一个对话框来创建一个Elman网络
net=newelm(PR,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF)
其中，PR为R组输入元素的最小值和最大值的设定值，Rx2维矩阵；Si为第i层的长度；TFi为第i层的传递函数，默认tansig；BTF为BP网络的训练函数，默认traingdx；BLF为BP网络的权值/阈值学习函数，默认learngdm；PF为性能函数，默认mse。
参数BTF可以取traingd、traingdm、traingda和traingdx等训练函数；BLF可以取学习函数learngd和learngdm；PF可以取性能函数mse和msereg。
利用newelm创建的Elman网络，权值函数采用dotprod，输入函数采用netsum，权值和阈值初始化函数采用initnw，训练函数采用trains，而传递函数和学习函数需要特别指定。

6. 径向基网络的神经网络工具箱函数：

径向基RBF网络是由Powell M.J.D于1985年提出的，以函数逼近理论为基础构造的一类前向网络。径向基函数网络只有两层，在中间层以对局部响应的径向基函数代替传统的全局响应的激发函数，有简单的结构、快速的训练过程及与权值无关的特性。由于局部响应的特性，对函数的逼近是最优的，训练过程很短，
MATLAB的神经网络工具箱为径向基网络提供了一些常用函数：

1）径向基神经网络创建函数：
⑴newrb：用来设计一个径向基网络
net=newrb %打开一个对话框来创建径向基神经网络
[net,tr]=newrb(P,T,GOAL,SPREAD,MN,DF)
其中，P为Q组输入向量组成的RxQ维矩阵；T为Q组目标分类向量组成的SxQ维矩阵；GOAL为均方误差，默认0；SPREAD为径向基的扩展速度，默认1；MN为神经元的最大数目，默认Q；DF为两次显示之间所添加的神经元数目，默认25；返回值net为一个径向基网络；返回值tr为训练记录。
newrb创建RBF网络是一个不断尝试的过程，创建过程中不断增加中间层神经元的个数，直到网络的输出误差满足预先设定的值为止。该函数设计的径向基网络net可用于函数逼近。径向基函数的扩展速度SPREAD越大，函数的拟合就越平滑，但需要非常多的神经元以适应函数的快速变化；如果过小就需要许多神经元来适应函数的缓慢变化，网络性能就不会很好。网络设计中，需要用不同的SPREAD值尝试，以确定一个最优值。
⑵newrbe：用于设计一个准确的径向基网络
net=newrbe %打开一个对话框来创建准确的径向基神经网络
net=newrbe(P,T,SPREAD)
其中参数含义见newrb说明。newrbe能够基于设计向量快速地、无误差地设计一个径向基网络。神经元数目越大，对函数的拟合就越平滑，但过多的神经元可能会导致计算困难。
⑶newpnn：用于创建概率神经网络
概率神经网络是一种适用于分类问题的径向基网络。
net=newpnn %打开一个对话框来创建概率神经网络
net=newpnn(P,T,SPREAD)
如果SPREAD值接近0，则创建的概率神经网络可以作为一个最近邻域分类器；随着SPREAD值的增大，需要更多考虑该网络附近的设计向量。
⑷newgrnn：用于设计一个广义回归神经网络
广义回归神经网络是径向基网络的一种，通常用于函数逼近。
net=newgrnn %打开一个对话框来创建广义回归神经网络
net=newgrnn(P,T,SPREAD)
SPREAD的值越大，由此设计的网络对函数的拟合就越平滑。为了更精确地对数据进行拟合，最好使SPREAD的值小于输入向量之间的典型距离。
2）转换函数：
⑴ind2vec：用于将数据索引转换为向量组
vec=ind2vec(ind)
其中，ind为数据索引列向量；函数返回值vec是一个稀疏矩阵，每行只有一个1，矩阵的行数等于数据索引的个数，列数等于数据索引中的最大值。
⑵vec2ind：用于将向量组转换为数据索引，与ind2vec是互逆的。
3）径向基传递函数。
A=radbas(N)
info=radbas(code)
其中，N为输入（列）向量的SxQ维矩阵；A为函数返回矩阵，与N一一对应，即N中的每一个元素通过径向基函数得到A。
info=radbas(code)根据code值返回有关函数的不同信息，返回导函数deriv；返回函数全称name；返回输入范围output；返回可用输入范围active。该函数的原型为：

7. 自组织竞争网络的神经网络工具箱函数：

自组织竞争神经网络以无教师教学方式进行网络训练，在训练过程中不需要期望值，而是根据输入数据的属性来调整权值，进而完成向环境学习、自动分类和聚类等任务。自组织竞争网络的基本思想是网络竞争层中的各神经元通过竞争来获取对输入模式的响应机会，最后仅剩一个输出最大的神经元称为竞争的胜利者，并对那些与获胜神经元有关的各连接权值朝着更有利于它竞争的方向调整。
MATLAB神经网络工具箱为自组织竞争网络提供的常用函数为：

1）自组织竞争网络创建函数：
⑴newc：用于创建一个竞争层
net=newc %打开一个对话框来创建一个竞争层
net=newc(PR,S,KLR,CLR)
其中，PR为R个输入元素的最大值和最小值的设定值，Rx2维矩阵；S为神经元数目；KLR为Kohonen学习速率，默认0.01；CLR为Conscience学习速率，默认0.001；返回值net为一个新的竞争层。
⑵newsom：用于创建一个自组织特征映射
net=newsom %打开一个对话框来创建一个自组织特征映射
net=newsom(PR,[d1,d2,...],tfcn,dfcn,olr,osteps,tlr,tns)
其中，PR为R个输入元素的最大值和最小值的设定值，Rx2维矩阵；di为第i层的维数，默认[5,8]；tfcn为拓扑函数，也即结构函数，默认hextop；dfcn为距离函数，默认linkdist；olr为分类阶段学习速率，默认0.9；osteps为分类阶段步长，默认1000；tlr为调谐阶段的学习速率，默认0.02；tns为调谐阶段的邻域距离，默认1；函数返回一个自组织特征映射。
⑶newlvq：用于创建一个学习向量量化LVQ网络
net=newlvq %打开一个对话框来创建一个学习向量量化LVQ网络
net=newlvq(PR,S1,PC,LR,LF)
其中，PR为Rx2矩阵，指定了输入向量中元素的最大值和最小值；S1为竞争层神经元数目；PC为分类的百分比；LR为学习速率，默认0.01；LF为学习函数，默认learnlv1。
学习函数LF可以选用learnlv1或learnlv2，但使用learnlv2是有限制的，只有在利用learnlv1对网络进行训练后，才可以调用learnlv2来结束训练。
2）传递函数：
⑴compet：为竞争性传递函数，用于神经元的网络输入转换
A=compet(N)
info=compet(code)
其中，N为输入（列向量）的SxQ维矩阵；返回值A为输出向量矩阵，每一列只有一个1，位于输入向量最大的位置。
info=compet(code)根据code值的不同返回有关函数的不同信息，返回导函数deriv，返回函数全称name，返回输出范围output，返回动态输入范围active。
⑵softmax：为软最大传递函数
A=softmax(N)
info=softmax(code)
其中，A为函数返回向量，各元素在区间[0 1]之间，且向量结构与N一致。
3）距离函数：
⑴boxdist：为Box距离函数，通常用于结构函数的gridtop的神经网络层
在给定神经网络某层的神经元位置后，可利用该函数计算神经元之间的距离。
d=boxdist(pos)
其中，pos为神经元位置的NxS维矩阵；函数返回值d为神经元距离的SxS维矩阵。
函数的运算原理为：

其中，d(i,j)表示距离矩阵中的元素；Pi表示位置矩阵的第i列向量。
⑵dist：为欧式距离权函数，通过对输入进行加权得到加权后的输入
Z=dist(W,P)
df=dist('deriv') %返回值为空，因为该函数不存在导函数
D=dist(pos)
其中，W为SxR维的权值矩阵；P为Q组输入（列）向量的RxQ维矩阵；Z为SxQ维的距离矩阵；pos为神经元位置的NxS维矩阵；D为SxS维的距离矩阵。
函数的运算规则为：

其中，x和y分别为列向量。
⑶linkdist：为连接距离函数
在给定神经元的位置后，该函数可用于计算神经元之间的距离。
d=linkdist(pos)
其中，pos为NxS维的神经元位置矩阵；d为SxS维的距离矩阵。函数运算原理为：

⑷mandist：为Manhattan距离权函数
Z=mandist(W,P)
df=mandist('deriv')
D=mandist(pos)
函数运算原理为：d=sum(abs(X-Y))，其中X和Y为两个向量
4）学习函数：
⑴learnk：为Kohonen权值学习函数
[dW,LS]=learnk(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
info=learnk(code)
其中，W为SxR维的权值矩阵，或S维的阈值向量；P为RxQ维的输入向量矩阵，也可用ones(1,Q)产生；Z为SxQ权值输入向量矩阵；N为SxQ网络输入向量矩阵；A为SxQ输出向量矩阵；T为SxQ层目标向量矩阵；E为SxQ层误差向量矩阵；gW为SxR性能梯度矩阵；gA为SxQ输出性能梯度矩阵；D为SxS神经元距离矩阵；LP为学习参数，若无则为空；LS为学习状态，初始化为空；返回值dW为SxR维的权值/阈值变化矩阵；返回值LS为新的学习状态。
info=learnk(code)根据不同的code值返回不同的相关信息，返回学习参数pnames，返回默认的学习参数pdefaults，函数使用了gW或gA时needg返回1。
在利用该函数进行学习之前，需要设定学习参数，例如学习速率设置LP.lr=0.01，这是学习速率的默认值。
函数利用Kohonen规则进行学习。Kohonen规则是竞争型神经网络常用的一种学习规则，这种学习规则只是调整一个神经元的权重，要求该神经元的权重和输入向量最匹配。
⑵learnsom：为自组织映射权值学习函数
[dW,LS]=learnsom(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
info=learnsom(code)
参数含义见learnk函数。在利用该函数进行学习之前，需要设置以下学习参数：

上述是MATLAB的默认值，如果需要调整，按上述格式重新设定即可。
⑶learnis：为Instar权值学习函数
[dW,LS]=learnis(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
info=learnis(code)
使用该函数前，需要设置学习速率，MATLAB默认值为LP.lr=0.01。
⑷learnos：为Outstar权值学习函数
[dW,LS]=learnos(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
5）初始化函数：
midpoint函数为中点权值初始化函数。
W=midpoint(S,PR)
其中，S为神经元的数目；PR为每组输入向量的最大值和最小值组成的Rx2维矩阵，规定了输入区间为[Pmin Pmax]；返回值W为SxR维矩阵，每个元素对应设定为(Pmin+Pmax)/2。
6）权值函数：
negdist函数为负距离权值函数。
Z=negdist(W,P)
df=negdist('deriv') %返回值为空，因为该函数的导函数不存在
其中，W为SxR维的权值矩阵；P为Q组输入向量的RxQ维矩阵。该函数的运算距离原理：

7）显示函数：
plotsom函数用于绘制自组织特征映射。
plotsom(pos) %利用红点绘制神经元的位置，将欧氏距离小于等于1的连接起来
plotsom(W,D,ND) %将欧氏距离小于等于1的神经元的权值向量连接起来
其中，pos为S个N维神经元的位置向量；W为权值矩阵；D为距离矩阵；ND为邻域矩阵，默认1。
8）结构函数：
⑴hextop：为六角层结构函数
pos=hextop(dim1,dim2,...,dimN)
其中，dimi为维数为i的层的长度；pos为N个并列向量组成的NxS维矩阵，S=dim1xdim2 x...xdimN。
⑵gridtop：为网格结构函数
pos=gridtop(dim1,dim2,...,dimN)
⑶randtop：为随机层结构函数
pos=randtop(dim1,dim2,...,dimN)
基本竞争型网络适合于解决模式分类问题。通过newc创建的基本竞争型神经网络只有一个竞争层，权值函数negdist，输入函数netsum，传递函数compet，初始化函数midpoint或initcon，训练函数或自适应函数为trains和trainr，学习函数为learnk或learncon。
利用基本竞争型网络进行分类，需要首先设定输入向量的类别总数，再由此确定神经元的个数。但利用SOM网络进行分类时，会自动将差别很小的点归为一类，差别不大的点激发的神经元位置也是邻近的。

8. GUI创建神经网络：

MATLAB中可以使用图形用户界面GUI（Graphical User Interfaces）来创建神经网络，在命令行中输入nntool后，会打开一个神经网络创建窗口。点击其中的New按钮，就可以创建打开一个创建神经网络的对话框，支持的创建类型Type有：Cascase-forward backprop、Competitive、Elman backprop、Feed-forward backprop、Feed-forward distributed time delay、Feed-forward time-delay、Generalized regression、Hopfield、Layer Recurrent、Linear layer、LVQ、NARX、NARX Series-Parallel、Perceptron、Probabilisttic、Radial basic、Self-organizing map。选择任何一种类型，就会显示对应类型神经网络的参数。这个界面还有一个Data书签，用于输入数据，包括Inputs、Targets、Input Delay States、Layer Delay States、Outputs、Errors等数据可供选择。

使用命令nnstart打开MATLAB提供的神经网络图形用户界面。使用命令nftool可以打开神经网络拟合工具箱图形界面，可用根据数据拟合函数。